Hand Image Classification – Part 1 – How many fingers?

Introduction

Image classification refers to classifying an image as being a member of a class of images. Examples include classifying an image in terms of whether the image is an image of a dog or not (binary classification) or whether the image is one of a dog, cat or neither (multi-class classification).

In this article, we:

develop a model to classify the number of fingers held up by a hand (multi-class)
improve on the model from Logistic Regression through Neural Networks (NN) and Convolutional Neural Networks (CNN)
make use of Transfer Learning to use what we have developed by applying it to a problem where we have to classify whether a hand is the Left hand or the Right hand (binary classification)

We will predominantly use Python for these tasks. The dataset we will be using is summarised next.

Fingers Dataset

The dataset at hand contains 21,600 images of hands holding up different numbers of fingers. In addition to the pixel contents of the image, each image is also labeled and that is encoded into the name of the file. Each image is of size 128 x 128 and has a black background and is in grey scale. This means each pixel has a single value representing its grey scale. Another way to say this is that each image has a single channel.

The task here is to develop a model, from simple to more advanced, that will determine the number of fingers held up in the image. To help assess the model’s performance on unseen data, 3,600 of the images from the dataset are put aside for testing the models’ predictive power.

The dataset is taken from kaggle here: https://www.kaggle.com/koryakinp/fingers/download

The contents of this article are:

Imports: We import all the required libraries. Notably, tensorflow and sklearn
Loading the data: In this section, we load the data and visualise it. We then save as a zipped pickle file to load it quicker the next time
Predicting the digit: Here we try to predict the number of fingers held up in the image
- Logistic Regression: We first use a simple logistic regression approach for a baseline performance
- Simple Logistic Regression Neural Network: This section replicates the Logistic Regression approach but as a Neural Network
- Deep Neural Network: This section looks to see if adding more fully connected layers helps at all to the performance beyond Logistic Regression
- Convolutional Nueral Network: The final section in predicting the digit looks at the benefits of Convolutions and normalisation
Predicting the hand: Here we try to predict which hand is held up in the image by using the model we have already built (Transfer Learning)

Imports

import Directory # for keeping a solid directory structure
import numpy as np
np.random.seed(101) # set random seed
import PIL # for reading in the png files
from matplotlib import image # for displaying the image files
import matplotlib.pyplot as plt

import pickle # for pickling the dataset so that it takes up less space
import bz2 # for compressing the dataset so that it takes up less space

import os
import time # to time some operations

from sklearn.linear_model import LogisticRegression
from sklearn import metrics

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.layers import Input,Dense,Activation,Dropout,Conv2D,Flatten,BatchNormalization
from tensorflow.keras.models import Model, load_model
from tensorflow.keras.utils import to_categorical

%matplotlib inline

Get rid of warnings:

import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings("ignore", category=ConvergenceWarning)

Global Variables

Any global variables used throughout this code, such as folder locations, are defined here

# setting up the folder paths for where the images are located
dir_image_folder_test = os.path.join(Directory.dataPath,'fingers','test')
dir_image_folder_train = os.path.join(Directory.dataPath,'fingers','train')

image_pickle_file = os.path.join(Directory.dataPath,'fingers_pickle.pkl.bzip')
model_h5_save = os.path.join(Directory.outputPath,'finger_count_model.h5')
model_h5_rlmodel_save = os.path.join(Directory.outputPath,'finger_count_model_rl.h5')

# this dictionary is to hold the datasets
fingers_dataset = None

Read in the pickle file if it exists

# start time
t0 = time.time()

try:
    infile = bz2.open(image_pickle_file,'rb')
except:
    print("Can't find pickle file. Will create it later: {}".format(image_pickle_file))
else:
    print("Loading compressed pickle file...")
    fingers_dataset = pickle.load(infile)
    infile.close()
    print("Compressed pickle file load complete!")
    
# print time taken
print(time.time() - t0, "seconds taken to run this cell")

Loading compressed pickle file…
Compressed pickle file load complete!
40.63017535209656 seconds taken to run this cell

Initial loading of the dataset

Here, we load up a single png file to see if we can successfully load it and visualise it. Later, we will read every file and store it.

# read in an example image (saves as a numpy array)
name = ''
if not os.path.isfile(image_pickle_file):
    data = image.imread(os.path.join(dir_image_folder_test,'000e7aa6-100b-4c6b-9ff0-e7a8e53e4465_5L.png'))
    name = '000e7aa6-100b-4c6b-9ff0-e7a8e53e4465_5L.png'
else:
    data = fingers_dataset['np_test']['X'][0]

# show some information about the data
print('name of file:{}'.format(name))
print('object:',type(data))
print('data type:',data.dtype)
print('shape:',data.shape)

print(data[0])

# display the image using the numpy array
plt.imshow(data)
plt.show()

name of file:
object: <class 'numpy.ndarray'>
data type: float32
shape: (128, 128)
[0.2784314  0.27450982 0.27450982 0.2784314  0.2901961  0.2901961
 0.27058825 0.26666668 0.26666668 0.2627451  0.24705882 0.24705882
 0.25490198 0.2509804  0.23921569 0.23921569 0.24705882 0.23529412
 0.2        0.1764706  0.17254902 0.18039216 0.20392157 0.21176471
 0.21176471 0.20784314 0.20392157 0.21176471 0.22352941 0.23137255
 0.23529412 0.22745098 0.20392157 0.19607843 0.19607843 0.19215687
 0.18039216 0.1764706  0.17254902 0.18039216 0.2        0.21176471
 0.21568628 0.21176471 0.19215687 0.1882353  0.2        0.20392157
 0.19607843 0.18431373 0.16862746 0.17254902 0.2        0.20784314
 0.19607843 0.19607843 0.20392157 0.21176471 0.21960784 0.21568628
 0.20784314 0.20784314 0.21176471 0.21176471 0.20784314 0.20784314
 0.21176471 0.21960784 0.22745098 0.23137255 0.22745098 0.22745098
 0.23921569 0.23529412 0.21960784 0.21960784 0.21960784 0.23137255
 0.2509804  0.2627451  0.26666668 0.25882354 0.24313726 0.23137255
 0.22745098 0.22745098 0.22745098 0.23921569 0.26666668 0.2627451
 0.23137255 0.21960784 0.22352941 0.21960784 0.20784314 0.20784314
 0.21960784 0.22352941 0.22745098 0.22352941 0.21568628 0.20392157
 0.19607843 0.2        0.21960784 0.22352941 0.20784314 0.20784314
 0.22352941 0.21960784 0.19607843 0.1882353  0.20392157 0.21568628
 0.22352941 0.23137255 0.23137255 0.23137255 0.23137255 0.22352941
 0.2        0.18431373 0.1764706  0.18039216 0.19215687 0.20784314
 0.21176471 0.21568628]

One of the images of a left hand holding up 5 fingers

Load all files

Here, we want to load all the files into an array if the pickle file doesn’t exist.

if fingers_dataset is None:
    # get a list of all the images that are in the directories
    dir_all_images_train = os.listdir(dir_image_folder_train)
    dir_all_images_test = os.listdir(dir_image_folder_test)

    # get the number of train/test examples
    i_train_examples_size = len(dir_all_images_train)
    i_test_examples_size = len(dir_all_images_test)

    print('Train files:',i_train_examples_size)
    print('Test files:',i_test_examples_size)
else:
    print('Data was already loaded. No need to load again.')

Data was already loaded. No need to load again.

# start time
t0 = time.time()

if fingers_dataset is None:
    # lists to store the images
    ls_train_X = []
    ls_train_digit = []
    ls_train_hand = []
    
    ls_test_X = []
    ls_test_digit = []
    ls_test_hand = []

    for img_name in dir_all_images_train:
        data = image.imread(os.path.join(dir_image_folder_train,img_name))
        digit = img_name.replace('.png','')[-2]
        hand = img_name.replace('.png','')[-1]
        ls_train_X.append(data)
        ls_train_digit.append(digit)
        ls_train_hand.append(hand)

    print('Train images loaded:',len(ls_train_X))

    for img_name in dir_all_images_test:
        data = image.imread(os.path.join(dir_image_folder_test,img_name))
        digit = img_name.replace('.png','')[-2]
        hand = img_name.replace('.png','')[-1]
        ls_test_X.append(data)
        ls_test_digit.append(digit)
        ls_test_hand.append(hand)

    print('Test images loaded:',len(ls_test_X))

    # convert to numpy arrays
    np_train_X = np.array(ls_train_X)
    np_test_X = np.array(ls_test_X)
    np_train_digit = np.array(ls_train_digit).reshape((-1,1))
    np_test_digit = np.array(ls_test_digit).reshape((-1,1))
    np_train_hand = np.array(ls_train_hand).reshape((-1,1))
    np_test_hand = np.array(ls_test_hand).reshape((-1,1))
    
    # save as a dictionary
    fingers_dataset = {'np_train':{'X':np_train_X,'digit':np_train_digit,'hand':np_train_hand},
                       'np_test':{'X':np_test_X,'digit':np_test_digit,'hand':np_test_hand}}
else:
    print('Data was already loaded. No need to load again.')
    
# print time taken
print(time.time() - t0, "seconds taken to run this cell")

Data was already loaded. No need to load again.
0.0 seconds taken to run this cell

# final shapes of our datasets
print('final train X shape:',fingers_dataset['np_train']['X'].shape)
print('final train digit shape:',fingers_dataset['np_train']['digit'].shape)
print('final train hand shape:',fingers_dataset['np_train']['hand'].shape)
print()
print('final test X shape:',fingers_dataset['np_test']['X'].shape)
print('final test digit shape:',fingers_dataset['np_test']['digit'].shape)
print('final test hand shape:',fingers_dataset['np_test']['hand'].shape)

final train X shape: (18000, 128, 128)
final train digit shape: (18000, 1)
final train hand shape: (18000, 1)

final test X shape: (3600, 128, 128)
final test digit shape: (3600, 1)
final test hand shape: (3600, 1)

# start time
t0 = time.time()

# save as a zipped pickle file if it doesn't already exist
if not os.path.isfile(image_pickle_file):
    print('Zipping the fingers dataset to: {}'.format(image_pickle_file))
    outputfile = bz2.BZ2File(image_pickle_file, 'w')
    pickle.dump(fingers_dataset,outputfile)
    outputfile.close()
else:
    print('The pickle file already exists. No need to create it again... Skipped.')
    
# print time taken
print(time.time() - t0, "seconds taken to run this cell")

The pickle file already exists. No need to create it again... Skipped.
0.0 seconds taken to run this cell

# let's check the unique values to make sure everything loaded correctly
print('Unique train digit values:',np.unique(np.squeeze(fingers_dataset['np_train']['digit'])))
print('Unique train hand values:',np.unique(np.squeeze(fingers_dataset['np_train']['hand'])))
print('Unique test digit values:',np.unique(np.squeeze(fingers_dataset['np_test']['digit'])))
print('Unique test hand values:',np.unique(np.squeeze(fingers_dataset['np_test']['hand'])))

Unique train digit values: ['0' '1' '2' '3' '4' '5']
Unique train hand values: ['L' 'R']
Unique test digit values: ['0' '1' '2' '3' '4' '5']
Unique test hand values: ['L' 'R']

Reshaping our dataset

def reshape_fingers_dataset(dict_fingers):
    # flatten the data set so that each example has an array of gray scale values
    x_train = dict_fingers['np_train']['X'].copy()
    x_train = x_train.reshape(x_train.shape[0],x_train.shape[1]*x_train.shape[2])

    y_train_digit = dict_fingers['np_train']['digit'].copy()
    y_train_digit = y_train_digit.reshape(-1,1)
    
    y_train_hand = dict_fingers['np_train']['hand'].copy()
    y_train_hand = y_train_hand.reshape(-1,1)

    x_test = dict_fingers['np_test']['X'].copy()
    x_test = x_test.reshape(x_test.shape[0],x_test.shape[1]*x_test.shape[2])

    y_test_digit = dict_fingers['np_test']['digit'].copy()
    y_test_digit = y_test_digit.reshape(-1,1)
    
    y_test_hand = dict_fingers['np_test']['hand'].copy()
    y_test_hand = y_test_hand.reshape(-1,1)

    print('The flattened train shape is:',x_train.shape)
    print('The flattened test shape is:',x_test.shape)

    print('The flattened train digit shape is:',y_train_digit.shape)
    print('The flattened test digit shape is:',y_test_digit.shape)
    print('The flattened train hand shape is:',y_train_hand.shape)
    print('The flattened test hand shape is:',y_test_hand.shape)
    
    return x_train,y_train_digit,y_train_hand,x_test,y_test_digit,y_test_hand

x_train,y_train_digit,y_train_hand,x_test,y_test_digit,y_test_hand = reshape_fingers_dataset(fingers_dataset)

The flattened train shape is: (18000, 16384)
The flattened test shape is: (3600, 16384)
The flattened train digit shape is: (18000, 1)
The flattened test digit shape is: (3600, 1)
The flattened train hand shape is: (18000, 1)
The flattened test hand shape is: (3600, 1)

Predicting the digit

Logistic Regression

Here, we apply a simple logistic regression to the flattened dataset to see how it fares. Classification. Reshaping for input into sklearn

def reshape_for_logistic_regression(x_train,y_train_value,m=None):
    if m is not None:
        x_train_lm = x_train.copy()[:m,:]
        y_train_lm = y_train_value.reshape(-1,)[:m]
    else:
        x_train_lm = x_train.copy()
        y_train_lm = y_train_value.reshape(-1,)
    
    return x_train_lm,y_train_lm

# WARNING! This cell takes a while

m = 2000

# start time
t0 = time.time()

# reshaping the response variable for sklearn. Limit the training to m examples to speed up
x_train_lm,y_train_lm = reshape_for_logistic_regression(x_train,y_train_digit,m=m)
x_test_lm,y_test_lm = reshape_for_logistic_regression(x_test,y_test_digit)

# get a LogisticRegression object
lm = LogisticRegression()

# fit it
lm.fit(x_train_lm, y_train_lm)

# print time taken
print(time.time() - t0, "seconds taken to run this cell")

17.39345693588257 seconds taken to run this cell

Let’s see how our simple logistic regression did.

# get the accuracy on the train set
score = lm.score(x_train_lm, y_train_lm)
print('The accuracy on the train set is:',score)

# get the accuracy on the test set
score = lm.score(x_test_lm, y_test_lm)
print('The accuracy on the test set is:',score)

print('Confusion Matrix')
predictions = lm.predict(x_test_lm)
metrics.confusion_matrix(y_test_lm,predictions)

The accuracy on the train set is: 1.0
The accuracy on the test set is: 0.9958333333333333
Confusion Matrix
array([[600, 0, 0, 0, 0, 0],
[ 0, 600, 0, 0, 0, 0],
[ 0, 4, 596, 0, 0, 0],
[ 0, 0, 7, 593, 0, 0],
[ 0, 0, 0, 0, 600, 0],
[ 0, 0, 0, 4, 0, 596]], dtype=int64)

This may look like really good performance. However, one way to assess classifier performance is relative to the Bayes Error. The Bayes Error is the hypothetical function which has the smallest possible error on this dataset. Humans are great at visualisation tasks and so we should use humans as a proxy to the Bayes Error rate.

Looking at the images this classifier classified incorrectly, humans would have no trouble getting these correct. It’s safe to assume that on this dataset, humans would be able to achieve a near 100% accuracy.

Suppose we’re dealing with a problem where we need no errors. It might be worth investigating whether a more complex model could result in a smaller error rate than this model.

First, let’s investigate the incorrectly classified images to see if there are any patterns.

def show_errors(x_test_lm,y_test_lm,predictions):
    x_incorrectly_classified = x_test_lm[(predictions != y_test_lm)]
    y_incorrectly_classified = y_test_lm[(predictions != y_test_lm)]
    y_predicted = predictions[(predictions != y_test_lm)]

    for i in range(len(y_predicted)):
        # display the image using the numpy array
        plt.imshow(x_incorrectly_classified[i].reshape((128,128)))
        plt.show()
        print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

show_errors(x_test_lm,y_test_lm,predictions)

There are 15 misclassifications, most of them are of the hands holding up a Three.

It looks like the errors are simply due to the inability of the model to adapt to complex shapes.

It is worth investigating whether the accuracy is improving as a function of the number of train examples given to it, i.e. the learning curve.

def logistic_regression_learning_curve(x_train,y_train_digit,x_test,y_test_digit,m=None,xlim=None,ylim=None,c=None, curve=True, single=False):

    # start with i = 10 training examples
    i = 10
    
    if m is None:
        m = len(x_train)
        
    if single:
        i = m

    # these are to save the performance
    acc_train = []
    acc_test = []
    i_train = []

    # the test set doesn't change
    x_test_lm,y_test_lm = reshape_for_logistic_regression(x_test,y_test_digit)

    # get a LogisticRegression object
    if c is None:
        lm = LogisticRegression()
    else:
        lm = LogisticRegression(C=c)

    while i <= m:
        # print progress
        print('{}/{}=>'.format(i,m), end='')

        # reshaping the response variable for sklearn
        x_train_lm,y_train_lm = reshape_for_logistic_regression(x_train,y_train_digit,m=i)

        # fit it
        lm.fit(x_train_lm, y_train_lm)

        # get the accuracy on the train set
        acc_train.append(lm.score(x_train_lm, y_train_lm))

        # get the accuracy on the train set
        acc_test.append(lm.score(x_test_lm, y_test_lm))

        # save the number of examples trained on
        i_train.append(i)

        # increase the train size by 10 initially and by 50 thereafter
        if i < 250:
            i += 10
        else:
            i += 50

    print()

    print('final train accuracy:',acc_train[-1])
    print('final test accuracy:',acc_test[-1])
    print('final train size:',i_train[-1])

    fig = None
    ax = None
    
    if curve:
        # plot the learning curve
        fig = plt.figure(figsize=(10,5))
        ax = fig.add_axes([0,0,1,1,])
        ax.plot(i_train,acc_test,label='Test',ls='solid')
        ax.plot(i_train,acc_train,label='Train',ls='solid')
        ax.set_xlim(xlim)
        ax.set_ylim(ylim)
        ax.legend()

    return lm, acc_train, acc_test, i_train, fig, ax

# WARNING! This cell takes a while

# start time
t0 = time.time()

lm, acc_train, acc_test, i_train, fig, ax = logistic_regression_learning_curve(x_train,y_train_digit,x_test,y_test_digit,m=3000,xlim=None,ylim=None)

# print time taken
print(time.time() - t0, "seconds taken to run this cell")

10/3000=>20/3000=>30/3000=>40/3000=>50/3000=>60/3000=>70/3000=>80/3000=>90/3000=>100/3000=>110/3000=>120/3000=>130/3000=>140/3000=>150/3000=>160/3000=>170/3000=>180/3000=>190/3000=>200/3000=>210/3000=>220/3000=>230/3000=>240/3000=>250/3000=>300/3000=>350/3000=>400/3000=>450/3000=>500/3000=>550/3000=>600/3000=>650/3000=>700/3000=>750/3000=>800/3000=>850/3000=>900/3000=>950/3000=>1000/3000=>1050/3000=>1100/3000=>1150/3000=>1200/3000=>1250/3000=>1300/3000=>1350/3000=>1400/3000=>1450/3000=>1500/3000=>1550/3000=>1600/3000=>1650/3000=>1700/3000=>1750/3000=>1800/3000=>1850/3000=>1900/3000=>1950/3000=>2000/3000=>2050/3000=>2100/3000=>2150/3000=>2200/3000=>2250/3000=>2300/3000=>2350/3000=>2400/3000=>2450/3000=>2500/3000=>2550/3000=>2600/3000=>2650/3000=>2700/3000=>2750/3000=>2800/3000=>2850/3000=>2900/3000=>2950/3000=>3000/3000=>
final train accuracy: 1.0
final test accuracy: 0.9983333333333333
final train size: 3000
619.3252651691437 seconds taken to run this cell

The accuracy of the model as a function of the number of data points used to train the model. We start with 10 training examples. We can see that after just 10 examples, the model is able to fit those examples for a perfect accuracy on the train set. However, is having trouble generalising to the test set. The accuracy on the test set reaches 99.8% when the entire 3000 data points are used for the train size. Note that the train set and the test set are distinct.

It’s quite difficult to see if the accuracy is still improving. We can have a closer look at the higher training sizes.

ax.set_xlim(1500)
ax.set_ylim(0.95)
fig

A resizing of the previous plot to zoom in to see if there is any improvement with increasing train set size.

It does look like it’s improving, with one less miss-classification at a time.

predictions = lm.predict(x_test_lm)
metrics.confusion_matrix(y_test_lm,predictions)

array([[600,   0,   0,   0,   0,   0],
       [  0, 600,   0,   0,   0,   0],
       [  0,   0, 600,   0,   0,   0],
       [  0,   0,   5, 595,   0,   0],
       [  0,   0,   0,   0, 600,   0],
       [  0,   0,   0,   1,   0, 599]], dtype=int64)

show_errors(x_test_lm,y_test_lm,predictions)

There are now 6 misclassifications, all but one of them are of the hands holding up a Three. By increasing our training size from 2000 to 3000, we have decreased our misclassifications from 15 to 6. However, the time taken to train went up from 17s to 619s.

It looks like 3s are often misclassified as 2s and the model hasn’t learned to classify 3s any better with a train size of 3000 with respect to 2000.

At this point we have a few actions we can take to improve the model on the test set:

Try hyperparameter tuning to get the most out of Logistic Regression
See if we can train on some more training data to see if we get an improvement
See if we can train a more complex model to see if we can improve on the misclassifications

1- Hyperparameter Tuning

Notice that the model has a 100% accuracy on the train set. This might mean that we are overfitting the train set. We can try to increase the L2-regularisation coefficient in an attempt to reduce this effect.

We know that the current coefficient (𝜆=1) overfits the train set. So we should be looking to increase the regularisation effect.

# WARNING! This cell takes a while

# start time
t0 = time.time()

m = 3000
acc_train = []
acc_test = []
c = np.linspace(start = 0.0001, stop = 1200, num = 10)/1000 # the smaller this value is, the more regularisation we are applying. It is the inverse of lambda coefficient

# reshaping the response variable for sklearn
# x_train_lm = x_train.copy()[:m,:]
# y_train_lm = y_train_digit.reshape(-1,)[:m]
# x_test_lm = x_test.copy()
# y_test_lm = y_test_digit.reshape(-1,)

x_train_lm,y_train_lm = reshape_for_logistic_regression(x_train,y_train_digit,m=m)
x_test_lm,y_test_lm = reshape_for_logistic_regression(x_test,y_test_digit)

for i in range(len(c)):
    # get a LogisticRegression object
    lm = LogisticRegression(C=c[i])

    # fit it
    lm.fit(x_train_lm, y_train_lm)

    # get the accuracy on the train set
    acc_train.append(lm.score(x_train_lm, y_train_lm))

    # get the accuracy on the test set
    acc_test.append(lm.score(x_test_lm, y_test_lm))
    
    print('{}/{}=>'.format(i+1,len(c)),end='')

print()

# plot the accuracy vs c
fig = plt.figure(figsize=(10,5))
ax = fig.add_axes([0,0,1,1,])
ax.plot(c,acc_test,label='Test',ls='solid')
ax.plot(c,acc_train,label='Train',ls='solid')
ax.legend()
ax.set_ylim(0.98)
    
# print time taken
print(time.time() - t0, "seconds taken to run this cell")

1/10=>2/10=>3/10=>4/10=>5/10=>6/10=>7/10=>8/10=>9/10=>10/10=>
139.71176171302795 seconds taken to run this cell

It looks like we can’t gain much from tuning the regularisation parameter.

2- Training on more training data

The reason we haven’t trained on the entirety of the training set (18k examples) is because of the memory and speed requirements for logistic regression (on my machine). We need a solution that will enable the model to be trained on more examples but without losing that much predictive power. We can explore shrinking the images (currently 128 by 128) to something like 28 by 28. Due to the relative simplicity of the images (held up fingers), we may be able to get away with shrinking the image with a pooling methodology.

One methodology we can apply is ‘Max Pooling’. This pooling approach can be used to reduce the size of the image (width and height) by summarising regions on the original images. Below, we see how Max Pooling using a window size of 2 by 2 and a stride of 2 can shrink a 10 by 10 image to a 5 by 5 image, effectively halving it. The maximum value is taken from each window as the window slides across by 2 steps going from the red window to the blue window until it reaches the end of that row. Then it slides 2 rows down.

There are also other Pooling methods such as ‘Average Pooling’.

We can use the max pooling function from Keras to do this for us. Below, we take the training examples and apply the above max pooling function with a filter/window of size 4 by 4 and a stride of 4 to reduce our 128 by 128 images to 32 by 32 images. We can then display them to see how they look after the transformation.

x_train_lm,y_train_lm = reshape_for_logistic_regression(x_train,y_train_digit)
x_test_lm,y_test_lm = reshape_for_logistic_regression(x_test,y_test_digit)

# for train
m,n_h,n_w = fingers_dataset['np_train']['X'].shape

# declare x as a tensorflow constant
x = tf.constant(x_train_lm)

# reshape the tensor to have 4 dimensions. The last dimension is called the 'channel' and is usually 3, for RGB values of each pixel
x = tf.reshape(x, [m,n_h,n_w, 1])

# this is our max pooling function we obtain as an object from keras
max_pool_2d = tf.keras.layers.MaxPooling2D(pool_size=(4, 4),strides=(4, 4), padding='valid')

# apply the transformation
x = max_pool_2d(x)

# convert it back to numpy
nparray = x.numpy()

m,n_h_new,n_w_new = nparray.shape[:3]

# reshape it back to how it was for linear regression
x_train_lm_transformed = nparray.reshape((m,n_h_new,n_w_new))

print('Transformed from {} to {}'.format((m,n_h,n_w),x_train_lm_transformed.shape))

Transformed from (18000, 128, 128) to (18000, 32, 32)

# for test
m,n_h,n_w = fingers_dataset['np_test']['X'].shape

# declare x as a tensorflow constant
x = tf.constant(x_test_lm)

# reshape the tensor to have 4 dimensions. The last dimension is called the 'channel' and is usually 3, for RGB values of each pixel
x = tf.reshape(x, [m,n_h,n_w, 1])

# this is our max pooling function we obtain as an object from keras
max_pool_2d = tf.keras.layers.MaxPooling2D(pool_size=(4, 4),strides=(4, 4), padding='valid')

# apply the transformation
x = max_pool_2d(x)

# convert it back to numpy
nparray = x.numpy()

m,n_h_new,n_w_new = nparray.shape[:3]

# reshape it back to how it was for linear regression
x_test_lm_transformed = nparray.reshape((m,n_h_new,n_w_new))

print('Transformed from {} to {}'.format((m,n_h,n_w),x_test_lm_transformed.shape))

Transformed from (3600, 128, 128) to (3600, 32, 32)

print('Before max pooling')
plt.imshow(x_train_lm[2].reshape((n_h,n_w)))
plt.show()

print('After max pooling')
plt.imshow(x_train_lm_transformed[2].reshape((n_h_new,n_w_new)))
plt.show()

Before max pooling

After max pooling

Now let’s apply logistic regresion to the entire dataset

# WARNING! This cell takes a while

# start time
t0 = time.time()

x_train_lm = x_train_lm_transformed.reshape((x_train_lm_transformed.shape[0],x_train_lm_transformed.shape[1]*x_train_lm_transformed.shape[2]))
y_train_lm = y_train_digit.reshape(-1,)
x_test_lm = x_test_lm_transformed.reshape((x_test_lm_transformed.shape[0],x_test_lm_transformed.shape[1]*x_test_lm_transformed.shape[2]))
y_test_lm = y_test_digit.reshape(-1,)

# get a LogisticRegression object
lm = LogisticRegression()

# fit it
lm.fit(x_train_lm, y_train_lm)

print('train accuracy:',lm.score(x_train_lm, y_train_lm))
print('test accuracy:',lm.score(x_test_lm, y_test_lm))
print('train size:',x_train_lm.shape[0])

# print time taken
print(time.time() - t0, "seconds taken to run this cell")

train accuracy: 1.0
test accuracy: 0.9994444444444445
train size: 18000
7.490400314331055 seconds taken to run this cell

The model runs a lot faster on this transformed dataset and attains an accuracy much closer to 100%. Let’s check out how many it misclassified.

predictions = lm.predict(x_test_lm)
metrics.confusion_matrix(y_test_lm,predictions)

array([[600,   0,   0,   0,   0,   0],
       [  0, 600,   0,   0,   0,   0],
       [  0,   0, 600,   0,   0,   0],
       [  0,   0,   2, 598,   0,   0],
       [  0,   0,   0,   0, 600,   0],
       [  0,   0,   0,   0,   0, 600]], dtype=int64)

The number of images that were misclassified is 2. This is great performance. We might be able to do better by specifying a smaller filter while using the max pooling function. We can see that below, these 2 images are a mirror of each other and one was probably generated from the other using data augmentation. In particular, it can be seen how an algorithm might have a hard time correctly classifying these images – one of the fingers is very close to the other. Applying a smaller filter would allow less ‘smudging’ of the grayscale values over the region.

x_incorrectly_classified = x_test_lm[(predictions != y_test_lm)]
y_incorrectly_classified = y_test_lm[(predictions != y_test_lm)]
y_predicted = predictions[(predictions != y_test_lm)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape((32,32)))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

For now, we leave this here and experiment with more complex algorithms to see whether we can get to a 100% accuracy

3- A more complex model

We now depart from Logistic Regression, which has done pretty well itself, to models more able to identify the features in the above misclassifications. We can start with a simple Neural Network with 1 layer, just an output layer. This will enable us to proceed with batch gradient descent which reduces the load on memory while retaining the learned weights/coefficients from batch to batch. The expectation is that no shrinking/transformation of the images will be necessary, resulting in no loss of image quality to leverage the full power of the model. If necessary, we may touch on Convolutional NNs as well.

Simple Logistic Regression Neural Network

The Logistic Regression application above performed poorly. The model we have used is not complex enough. NNs might do better. But let’s try to replicate the performance of the logistic regression with a Neural Network. Note that the logistic regression classifier from SKlearn automatically uses a regularisation coefficient of 1. First let’s see the performance of Logistic Regression with 0 (very nearly 0) regularisation

# WARNING! This cell takes a while

# start time
t0 = time.time()

logistic_regression_learning_curve(x_train,y_train_digit,x_test,y_test_digit,m=3000,xlim=None,ylim=None, single=True, curve=False,c=100000000000000)

# print time taken
print(time.time() - t0, "seconds taken to run this cell")

3000/3000=>
final train accuracy: 1.0
final test accuracy: 0.9941666666666666
final train size: 3000
9.156294822692871 seconds taken to run this cell

We can replicate Logistic Regression with a single layer Neural Network. The image below summarises our architecture:

Input Layer: This is our 128 x 128 image flattened out to 16,384 neurons
Output Layer: This is the output of the Neural Network. There should be 6 outputs – each corresponding to the number of fingers held up.
Weights and Bias: As with Logistic Regression, we have that the value in the first neuron of the output layer for example 𝑖 is: $A_0^{(i)} = g(W[0]X^{(i)} + B[0])$ where g is the activation function, $W[0]$ is the first row of the $6 \times 16,384$ weights matrix and $B[0]$ is the first element of the $6 \times 16$ bias vector.
Activation: For multiclass classification we have the Softmax function. For the $k^{kth}$ output $\hat{Y}_k^{(i)}$ this is: $\frac{e^{x_k}}{\sum_{i=1}^n e^{x_i}}$ .
Loss Function: For multiclass classification, the loss of a single example, $i$ , would be $L(Y^{(i)},\hat{Y}^{(i)}) = -\sum^5_{k=0} Y^{(i)}_k log \left(\hat{Y}^{(i)}_k \right)$ . This is the Multinomial/Categorical Cross Entropy Loss. For only 2 classes, this is equivalent to the Binomial Cross entropy which may be more familiar:

$L(Y^{(i)},\hat{Y}^{(i)}) = -\sum^2_k Y^{(i)}_k log \left(\hat{Y}^{(i)}_k \right) = -Y^{(i)}_0 log \left(\hat{Y}^{(i)}_0 \right) - Y^{(i)}_1 log \left(\hat{Y}^{(i)}_1 \right) = -Y^{(i)}_0 log \left(\hat{Y}^{(i)}_0 \right) - (1-Y^{(i)}_0) log \left(1- \hat{Y}^{(i)}_0 \right)$

where $\hat{Y}^{(i)}_1=1- \hat{Y}^{(i)}_0$ . The Cost function for the Categorical Loss is then the average Loss over the set of examples:

$J(Y^{(i)},\hat{Y}^{(i)}) = \frac{1}{n} \sum^n_{i=0} L(Y^{(i)},\hat{Y}^{(i)})$

A Neural Network with a single layer (an output layer). Each neuron in the output layer is a linear combination of the input layer weighted by a set of weights (W), fed into an activation function, g (here g is the softmax function). Here, g is shown as applying to each neuron individually, however, the denominator of the softmax function is a sum over all the output layers which acts to ensure the output layer’s probabilities sum to 1.

Below, we limit our training set size to 3000 as we did for Logistic Regression above. Since the labels are categorical, we encode them as a vector. For example, if an image has label ‘4’, we encode this as [0,0,0,0,1,0], where there is a ‘1’ in the element corresponding to 4 fingers (indexing starts at 0).

m = 3000

# getting the train and test set
x_train_nn = x_train.copy()[:m]
y_train_nn = to_categorical(y_train_digit)[:m]
x_test_nn = x_test.copy()
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(x_train_nn.shape[1:])

# adding a fully connected layer with the same activation function as that in logistic regression for multiple classes
X = Dense(6, activation='softmax', name='fc')(X_input)

# the model
model = Model(inputs = X_input, outputs = X, name='SimpleLogisticRegressionNNModel')

# compile with adam optimiser and categorical cross entropy as the loss function
model.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])

print(x_train_nn.shape,y_train_nn.shape)

# fit
model.fit(x_train_nn,y_train_nn,batch_size=16,epochs=20)

(3000, 16384) (3000, 6)
Train on 3000 samples
Epoch 1/20
3000/3000 [==============================] - 4s 1ms/sample - loss: 0.6567 - accuracy: 0.8117
Epoch 2/20
3000/3000 [==============================] - 1s 200us/sample - loss: 0.1491 - accuracy: 0.9633
Epoch 3/20
3000/3000 [==============================] - 1s 216us/sample - loss: 0.0793 - accuracy: 0.9860
Epoch 4/20
3000/3000 [==============================] - 1s 210us/sample - loss: 0.0658 - accuracy: 0.9873
Epoch 5/20
3000/3000 [==============================] - 1s 230us/sample - loss: 0.0498 - accuracy: 0.9897
Epoch 6/20
3000/3000 [==============================] - 1s 222us/sample - loss: 0.0412 - accuracy: 0.9907
Epoch 7/20
3000/3000 [==============================] - 1s 230us/sample - loss: 0.0610 - accuracy: 0.9803
Epoch 8/20
3000/3000 [==============================] - 1s 249us/sample - loss: 0.0269 - accuracy: 0.9930
Epoch 9/20
3000/3000 [==============================] - 1s 260us/sample - loss: 0.0179 - accuracy: 0.9970
Epoch 10/20
3000/3000 [==============================] - 1s 249us/sample - loss: 0.0191 - accuracy: 0.9973
Epoch 11/20
3000/3000 [==============================] - 1s 247us/sample - loss: 0.0117 - accuracy: 0.9980
Epoch 12/20
3000/3000 [==============================] - 1s 204us/sample - loss: 0.0165 - accuracy: 0.9970
Epoch 13/20
3000/3000 [==============================] - 1s 232us/sample - loss: 0.0078 - accuracy: 0.9997
Epoch 14/20
3000/3000 [==============================] - 1s 227us/sample - loss: 0.0061 - accuracy: 1.0000
Epoch 15/20
3000/3000 [==============================] - 1s 224us/sample - loss: 0.0073 - accuracy: 0.9997
Epoch 16/20
3000/3000 [==============================] - 1s 230us/sample - loss: 0.0281 - accuracy: 0.9890
Epoch 17/20
3000/3000 [==============================] - 1s 246us/sample - loss: 0.1315 - accuracy: 0.9667
Epoch 18/20
3000/3000 [==============================] - 1s 212us/sample - loss: 0.0027 - accuracy: 1.0000
Epoch 19/20
3000/3000 [==============================] - 1s 224us/sample - loss: 0.0024 - accuracy: 1.0000
Epoch 20/20
3000/3000 [==============================] - 1s 219us/sample - loss: 0.0059 - accuracy: 0.9983

Similar to Logistic Regression, we have a train set accuracy of 100% as seen below.

preds = model.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

Train set accuracy: 1.0
Test set accuracy: 0.9936111

Our Neural Network is also having problems with classifying 3s as we can see with the misclassifications below.

# get the actual predicted probabilities from the model on the test set
preds = model.predict(x_test_nn)

# use the actual probabilities to classify as the class with the greatest probability, i.e. [0,0,0,1,0,0] -> 3
pred_classes = tf.argmax(preds, axis=1)

# convert to numpy array
predictions = pred_classes.numpy()

# encode the labels back to single numbers, i.e. [0,0,0,1,0,0] -> 3
actuals = tf.argmax(y_test_nn, axis=1).numpy()

# get the incorrectly classified images
x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

# display each one
for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

There are 23 misclassifications in total – almost all 3s.

If we now use the entire train set, we expect a better performance than our Logistic Regression above since in order to use Logistic Regression over the entire dataset, we had to shrink our images from 128 x 128 to 32 x 32. It is likely that we lost some important details in that transformation.

# getting the train and test set
x_train_nn = x_train.copy()
y_train_nn = to_categorical(y_train_digit)
x_test_nn = x_test.copy()
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(x_train_nn.shape[1:])

# adding a fully connected layer with the same activation function as that in logistic regression for multiple classes
X = Dense(6, activation='softmax', name='fc')(X_input)

# the model
model = Model(inputs = X_input, outputs = X, name='SimpleLogisticRegressionNNModel')

# compile
model.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])

print(x_train_nn.shape,y_train_nn.shape)

# fit
model.fit(x_train_nn,y_train_nn,batch_size=32,epochs=20)

preds = model.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

preds = model.predict(x_test_nn)
predictions = tf.argmax(preds, axis=1).numpy()
actuals = tf.argmax(y_test_nn, axis=1).numpy()

x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

(18000, 16384) (18000, 6)
Train on 18000 samples
Epoch 1/20
18000/18000 [==============================] - 3s 162us/sample - loss: 0.2582 - accuracy: 0.9371
Epoch 2/20
18000/18000 [==============================] - 3s 150us/sample - loss: 0.0420 - accuracy: 0.9942
Epoch 3/20
18000/18000 [==============================] - 3s 145us/sample - loss: 0.0175 - accuracy: 0.9980
Epoch 4/20
18000/18000 [==============================] - 3s 148us/sample - loss: 0.0131 - accuracy: 0.9986
Epoch 5/20
18000/18000 [==============================] - 3s 148us/sample - loss: 0.0072 - accuracy: 0.9996
Epoch 6/20
18000/18000 [==============================] - 3s 149us/sample - loss: 0.0052 - accuracy: 0.9999
Epoch 7/20
18000/18000 [==============================] - 3s 149us/sample - loss: 0.0069 - accuracy: 0.9987
Epoch 8/20
18000/18000 [==============================] - 3s 146us/sample - loss: 0.0247 - accuracy: 0.9926
Epoch 9/20
18000/18000 [==============================] - 3s 152us/sample - loss: 0.0032 - accuracy: 0.9992
Epoch 10/20
18000/18000 [==============================] - 3s 150us/sample - loss: 0.0016 - accuracy: 0.9998
Epoch 11/20
18000/18000 [==============================] - 3s 147us/sample - loss: 9.8493e-04 - accuracy: 1.0000
Epoch 12/20
18000/18000 [==============================] - 3s 149us/sample - loss: 5.5767e-04 - accuracy: 1.0000
Epoch 13/20
18000/18000 [==============================] - 3s 148us/sample - loss: 5.2865e-04 - accuracy: 1.0000
Epoch 14/20
18000/18000 [==============================] - 3s 150us/sample - loss: 4.2136e-04 - accuracy: 1.0000
Epoch 15/20
18000/18000 [==============================] - 3s 147us/sample - loss: 0.0062 - accuracy: 0.9988
Epoch 16/20
18000/18000 [==============================] - 3s 149us/sample - loss: 0.0316 - accuracy: 0.9921
Epoch 17/20
18000/18000 [==============================] - 3s 148us/sample - loss: 3.0205e-04 - accuracy: 1.0000
Epoch 18/20
18000/18000 [==============================] - 3s 147us/sample - loss: 2.8135e-04 - accuracy: 1.0000
Epoch 19/20
18000/18000 [==============================] - 3s 150us/sample - loss: 2.0796e-04 - accuracy: 1.0000
Epoch 20/20
18000/18000 [==============================] - 3s 147us/sample - loss: 1.8522e-04 - accuracy: 1.0000
Train set accuracy: 1.0
Test set accuracy: 0.9994444

We only have 2 misclassifications. We are still misclassifying a couple of 3s. Let us see whether adding one more layer helps improve the classification. The architecture is as below:

Vanilla Deep Neural Networks

This is a 2-layers Neural Network. The output layer still had a softmac activation function but the hidden layer that has been added has a ReLU activation function.

This architecture still fails to improve the accuracy as seen below:

# getting the train and test set
x_train_nn = x_train.copy()
y_train_nn = to_categorical(y_train_digit)
x_test_nn = x_test.copy()
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(x_train_nn.shape[1:])

# adding a fully connected layer
X = Dense(128, activation='relu', name='fc')(X_input)

# adding another fully connected layer
X = Dense(6, activation='softmax', name='fc2')(X)

# the model
model = Model(inputs = X_input, outputs = X, name='SimpleLogisticRegressionNNModel1')

# compile
model.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])
print(x_train_nn.shape,y_train_nn.shape)
# fit
model.fit(x_train_nn,y_train_nn,batch_size=32,epochs=20)

preds = model.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

predictions = model.predict(x_test_nn)
predictions = tf.argmax(predictions, axis=1).numpy()
actuals = tf.argmax(y_test_nn, axis=1).numpy()

x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

(18000, 16384) (18000, 6)
Train on 18000 samples
Epoch 1/20
18000/18000 [==============================] - 10s 548us/sample - loss: 0.2890 - accuracy: 0.9355
Epoch 2/20
18000/18000 [==============================] - 9s 496us/sample - loss: 0.0298 - accuracy: 0.9946
Epoch 3/20
18000/18000 [==============================] - 9s 500us/sample - loss: 0.0107 - accuracy: 0.9986
Epoch 4/20
18000/18000 [==============================] - 9s 498us/sample - loss: 0.0059 - accuracy: 0.9992
Epoch 5/20
18000/18000 [==============================] - 9s 486us/sample - loss: 0.0028 - accuracy: 0.9998
Epoch 6/20
18000/18000 [==============================] - 9s 488us/sample - loss: 0.0352 - accuracy: 0.9912
Epoch 7/20
18000/18000 [==============================] - 9s 489us/sample - loss: 0.0023 - accuracy: 0.9996
Epoch 8/20
18000/18000 [==============================] - 9s 511us/sample - loss: 9.2688e-04 - accuracy: 1.0000
Epoch 9/20
18000/18000 [==============================] - 9s 523us/sample - loss: 7.9297e-04 - accuracy: 1.0000
Epoch 10/20
18000/18000 [==============================] - 9s 503us/sample - loss: 0.0330 - accuracy: 0.9917TA: 0s - loss: 0.0
Epoch 11/20
18000/18000 [==============================] - 9s 513us/sample - loss: 0.0036 - accuracy: 0.9988
Epoch 12/20
18000/18000 [==============================] - 10s 531us/sample - loss: 0.0022 - accuracy: 0.9994
Epoch 13/20
18000/18000 [==============================] - 9s 510us/sample - loss: 0.0012 - accuracy: 0.9996
Epoch 14/20
18000/18000 [==============================] - 9s 500us/sample - loss: 9.6602e-04 - accuracy: 0.9997
Epoch 15/20
18000/18000 [==============================] - 9s 498us/sample - loss: 2.6138e-04 - accuracy: 1.0000
Epoch 16/20
18000/18000 [==============================] - 9s 499us/sample - loss: 2.3768e-04 - accuracy: 1.0000
Epoch 17/20
18000/18000 [==============================] - 9s 501us/sample - loss: 1.9344e-04 - accuracy: 1.0000
Epoch 18/20
18000/18000 [==============================] - 9s 525us/sample - loss: 0.0436 - accuracy: 0.9896
Epoch 19/20
18000/18000 [==============================] - 9s 513us/sample - loss: 0.0020 - accuracy: 0.9993
Epoch 20/20
18000/18000 [==============================] - 9s 491us/sample - loss: 4.5319e-04 - accuracy: 1.0000
Train set accuracy: 1.0
Test set accuracy: 0.9994444

Even adding a few more layers doesn’t help get a perfect classification

# getting the train and test set
x_train_nn = x_train.copy()
y_train_nn = to_categorical(y_train_digit)
x_test_nn = x_test.copy()
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(x_train_nn.shape[1:])

# # add a dropout layer
# X = Dropout(0.3)

# adding a fully connected layer
X = Dense(128, activation='relu', name='fc')(X_input)

# add a dropout layer
# X = Dropout(0.3)

# adding a fully connected layer
X = Dense(64, activation='relu', name='fc2')(X)

# add a dropout layer
# X = Dropout(0.3)

# adding a fully connected layer
X = Dense(32, activation='relu', name='fc3')(X)

# add a dropout layer
# X = Dropout(0.3)

# adding another fully connected layer
X = Dense(6, activation='softmax', name='fc4')(X)

# the model
model_NN = Model(inputs = X_input, outputs = X, name='SimpleLogisticRegressionNNModel2')

# compile
model_NN.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])
print(x_train_nn.shape,y_train_nn.shape)
# fit
model_NN.fit(x_train_nn,y_train_nn,batch_size=64,epochs=20)

preds = model_NN.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model_NN.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

predictions = model_NN.predict(x_test_nn)
predictions = tf.argmax(predictions, axis=1).numpy()
actuals = tf.argmax(y_test_nn, axis=1).numpy()

x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

(18000, 16384) (18000, 6)
Train on 18000 samples
Epoch 1/20
18000/18000 [==============================] - 7s 370us/sample - loss: 0.3847 - accuracy: 0.8872 - loss: 0.3874 - accuracy: 0.88
Epoch 2/20
18000/18000 [==============================] - 6s 329us/sample - loss: 0.0260 - accuracy: 0.9951
Epoch 3/20
18000/18000 [==============================] - 6s 332us/sample - loss: 0.0176 - accuracy: 0.9952
Epoch 4/20
18000/18000 [==============================] - 6s 327us/sample - loss: 0.0684 - accuracy: 0.9793
Epoch 5/20
18000/18000 [==============================] - 6s 337us/sample - loss: 0.0091 - accuracy: 0.9973
Epoch 6/20
18000/18000 [==============================] - 6s 331us/sample - loss: 0.0039 - accuracy: 0.9988
Epoch 7/20
18000/18000 [==============================] - 6s 325us/sample - loss: 0.0025 - accuracy: 0.9992
Epoch 8/20
18000/18000 [==============================] - 6s 323us/sample - loss: 7.6914e-04 - accuracy: 0.9999 - loss: 8.1420e
Epoch 9/20
18000/18000 [==============================] - 6s 321us/sample - loss: 0.0011 - accuracy: 0.9997
Epoch 10/20
18000/18000 [==============================] - 6s 325us/sample - loss: 3.7986e-04 - accuracy: 1.0000
Epoch 11/20
18000/18000 [==============================] - 6s 329us/sample - loss: 2.0658e-04 - accuracy: 1.0000
Epoch 12/20
18000/18000 [==============================] - 6s 321us/sample - loss: 1.9072e-04 - accuracy: 1.0000
Epoch 13/20
18000/18000 [==============================] - 6s 328us/sample - loss: 1.4158e-04 - accuracy: 1.0000
Epoch 14/20
18000/18000 [==============================] - 6s 329us/sample - loss: 1.0618e-04 - accuracy: 1.0000
Epoch 15/20
18000/18000 [==============================] - 6s 326us/sample - loss: 1.2138e-04 - accuracy: 1.0000
Epoch 16/20
18000/18000 [==============================] - 6s 323us/sample - loss: 9.7069e-05 - accuracy: 1.0000
Epoch 17/20
18000/18000 [==============================] - 6s 326us/sample - loss: 5.7578e-05 - accuracy: 1.0000
Epoch 18/20
18000/18000 [==============================] - 6s 323us/sample - loss: 0.1185 - accuracy: 0.9789
Epoch 19/20
18000/18000 [==============================] - 6s 323us/sample - loss: 0.0022 - accuracy: 0.9998
Epoch 20/20
18000/18000 [==============================] - 6s 330us/sample - loss: 8.3741e-04 - accuracy: 0.9999
Train set accuracy: 1.0
Test set accuracy: 0.99972224

Notice that there is a stability issue in the optimisation. Namely, the loss fluctuates at times. We can try to add a batch normalisation (https://arxiv.org/pdf/1502.03167v2.pdf) step to help the algorithm approach/converge to the global minimum in a more stable manner (Note that the nature of mini-batch training might introduce such a symptom of loss fluctuation but in general the loss should be improving.)

# getting the train and test set
x_train_nn = x_train.copy()
y_train_nn = to_categorical(y_train_digit)
x_test_nn = x_test.copy()
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(x_train_nn.shape[1:])

# # add a dropout layer
# X = Dropout(0.3)

# adding a fully connected layer
X = Dense(128, name='fc')(X_input)
X = BatchNormalization(axis=1)(X) # normalise across axis 1. Axis 0 is the batch size and axis 1 is the activations
X = Activation('relu')(X)

# add a dropout layer
# X = Dropout(0.3)

# adding a fully connected layer
X = Dense(64, name='fc2')(X)
X = BatchNormalization(axis=1)(X)
X = Activation('relu')(X)

# add a dropout layer
# X = Dropout(0.3)

# adding a fully connected layer
X = Dense(32, name='fc3')(X)
X = BatchNormalization(axis=1)(X)
X = Activation('relu')(X)

# add a dropout layer
# X = Dropout(0.3)

# adding another fully connected layer
X = Dense(6, activation='softmax', name='fc4')(X)

# the model
model_NN_batchNorm = Model(inputs = X_input, outputs = X, name='NNModel_with_batch_norm')

# compile
model_NN_batchNorm.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])
print(x_train_nn.shape,y_train_nn.shape)
# fit
model_NN_batchNorm.fit(x_train_nn,y_train_nn,batch_size=64,epochs=20)

preds = model_NN_batchNorm.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model_NN_batchNorm.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

predictions = model_NN_batchNorm.predict(x_test_nn)
predictions = tf.argmax(predictions, axis=1).numpy()
actuals = tf.argmax(y_test_nn, axis=1).numpy()

x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

(18000, 16384) (18000, 6)
Train on 18000 samples
Epoch 1/20
18000/18000 [==============================] - 8s 460us/sample - loss: 0.0973 - accuracy: 0.9861
Epoch 2/20
18000/18000 [==============================] - 6s 341us/sample - loss: 0.0098 - accuracy: 0.9992
Epoch 3/20
18000/18000 [==============================] - 6s 341us/sample - loss: 0.0025 - accuracy: 1.0000
Epoch 4/20
18000/18000 [==============================] - 6s 340us/sample - loss: 0.0013 - accuracy: 1.0000
Epoch 5/20
18000/18000 [==============================] - 6s 344us/sample - loss: 0.0010 - accuracy: 1.0000
Epoch 6/20
18000/18000 [==============================] - 6s 340us/sample - loss: 0.0094 - accuracy: 0.9976
Epoch 7/20
18000/18000 [==============================] - 6s 341us/sample - loss: 0.0030 - accuracy: 0.9994 - loss: 0.0 - ETA: 0s -
Epoch 8/20
18000/18000 [==============================] - 6s 339us/sample - loss: 0.0018 - accuracy: 0.9993
Epoch 9/20
18000/18000 [==============================] - 6s 342us/sample - loss: 0.0017 - accuracy: 0.9994
Epoch 10/20
18000/18000 [==============================] - 6s 348us/sample - loss: 8.3171e-04 - accuracy: 0.9999
Epoch 11/20
18000/18000 [==============================] - 6s 343us/sample - loss: 2.0734e-04 - accuracy: 1.0000 - loss: 2.1434e-0
Epoch 12/20
18000/18000 [==============================] - 6s 348us/sample - loss: 2.0509e-04 - accuracy: 1.0000
Epoch 13/20
18000/18000 [==============================] - 6s 342us/sample - loss: 1.1689e-04 - accuracy: 1.0000
Epoch 14/20
18000/18000 [==============================] - 6s 347us/sample - loss: 8.5498e-05 - accuracy: 1.0000
Epoch 15/20
18000/18000 [==============================] - 6s 341us/sample - loss: 4.8263e-04 - accuracy: 0.9999
Epoch 16/20
18000/18000 [==============================] - 6s 341us/sample - loss: 0.0075 - accuracy: 0.9981
Epoch 17/20
18000/18000 [==============================] - 6s 349us/sample - loss: 0.0018 - accuracy: 0.9997
Epoch 18/20
18000/18000 [==============================] - 7s 367us/sample - loss: 0.0017 - accuracy: 0.9996
Epoch 19/20
18000/18000 [==============================] - 7s 379us/sample - loss: 0.0041 - accuracy: 0.9989
Epoch 20/20
18000/18000 [==============================] - 7s 375us/sample - loss: 3.7911e-04 - accuracy: 0.9999
Train set accuracy: 1.0
Test set accuracy: 0.99972224

We still do not have 100% accuracy as well as stability in the above model. The accuracy tends to fluctuate. We’d like to arrive at a solution which is more stable in terms of the accuracy. Next we’ll see if Convolutional networks can deliver us 100% accuracy while being a bit more stable.

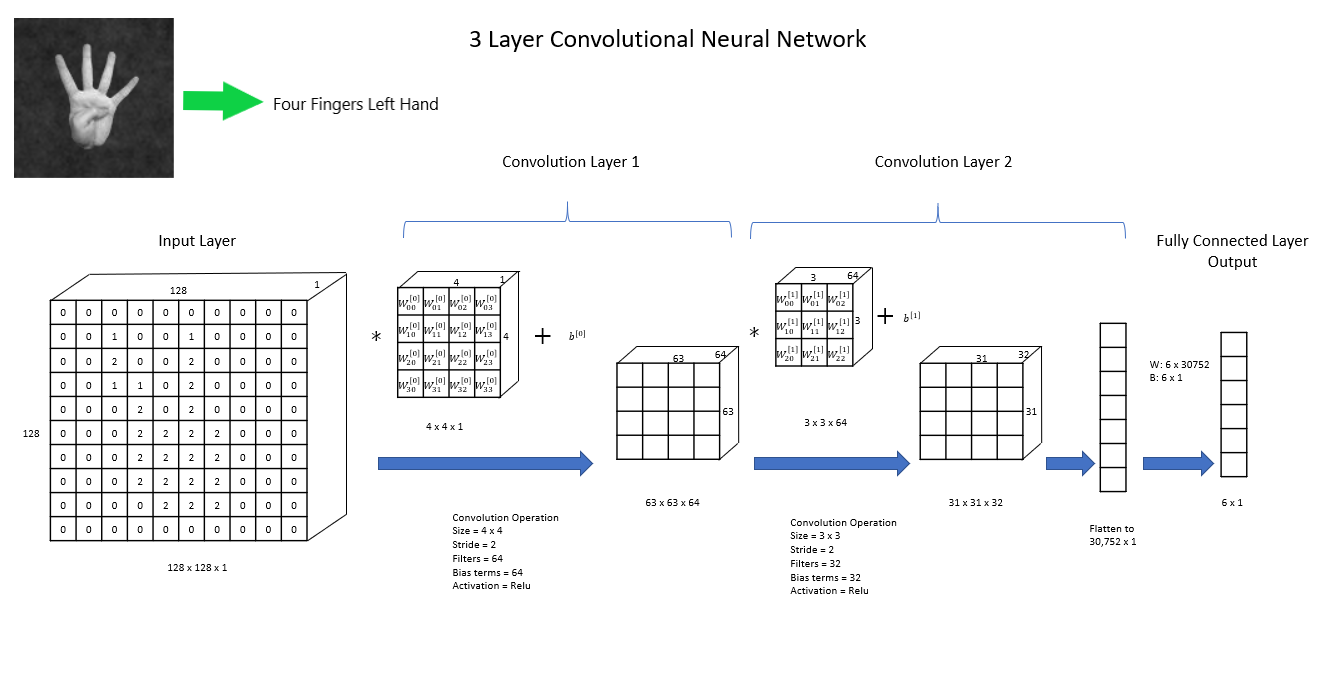
Convolutional Neural Networks

Below we implement a 3-Layer Convolutional Neural Network. Remember that we’re after a more stable accuracy on the training set. Our architecture looks like this:

This is a 3-layer Convolutional Neural Network. Each convolution layer applies a convolution operation then adds a bias term resulting in a matrix of reduced size to be fed to the next layer. The second convolution layer has an additional transformation component to transform the matrix to array with 1 column. The final layer is not a convolution layer, it is a fully connected layer with a softmax activation function to predict one of 6 classes.

# getting the train and test set
x_train_nn = fingers_dataset['np_train']['X'].copy()
x_train_nn = x_train_nn.reshape((x_train_nn.shape[0],x_train_nn.shape[1],x_train_nn.shape[2],1))
y_train_nn = to_categorical(y_train_digit)
x_test_nn = fingers_dataset['np_test']['X'].copy()
x_test_nn = x_test_nn.reshape((x_test_nn.shape[0],x_test_nn.shape[1],x_test_nn.shape[2],1))
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(shape=(x_train_nn.shape[1:]))

# convolutional layer
X = Conv2D(64,kernel_size=4,strides=2)(X_input)
X = Activation('relu')(X)

# convolutional layer
X = Conv2D(32,kernel_size=3,strides=2)(X)
X = Activation('relu')(X)

X = Flatten()(X)

# adding another fully connected layer
X = Dense(6, activation='softmax', name='fc')(X)

# the model
model_CNN = Model(inputs = X_input, outputs = X, name='CNNModel')

# compile
model_CNN.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])
print(x_train_nn.shape,y_train_nn.shape)
# fit
model_CNN.fit(x_train_nn,y_train_nn,batch_size=32,epochs=20)

preds = model_CNN.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model_CNN.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

predictions = model_CNN.predict(x_test_nn)
predictions = tf.argmax(predictions, axis=1).numpy()
actuals = tf.argmax(y_test_nn, axis=1).numpy()

x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

(18000, 128, 128, 1) (18000, 6)
Train on 18000 samples
Epoch 1/20
18000/18000 [==============================] - 83s 5ms/sample - loss: 0.1146 - accuracy: 0.9642
Epoch 2/20
18000/18000 [==============================] - 84s 5ms/sample - loss: 0.0023 - accuracy: 0.9994
Epoch 3/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 1.0560e-04 - accuracy: 1.0000
Epoch 4/20
18000/18000 [==============================] - 81s 5ms/sample - loss: 5.7496e-05 - accuracy: 1.0000
Epoch 5/20
18000/18000 [==============================] - 82s 5ms/sample - loss: 1.6847e-05 - accuracy: 1.0000
Epoch 6/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 1.3621e-05 - accuracy: 1.0000
Epoch 7/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 7.9775e-06 - accuracy: 1.0000
Epoch 8/20
18000/18000 [==============================] - 80s 4ms/sample - loss: 6.5643e-06 - accuracy: 1.0000
Epoch 9/20
18000/18000 [==============================] - 80s 4ms/sample - loss: 4.1088e-06 - accuracy: 1.0000
Epoch 10/20
18000/18000 [==============================] - 81s 5ms/sample - loss: 9.3047e-06 - accuracy: 1.0000
Epoch 11/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 0.0179 - accuracy: 0.9964
Epoch 12/20
18000/18000 [==============================] - 82s 5ms/sample - loss: 7.7671e-05 - accuracy: 1.0000
Epoch 13/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 2.7739e-05 - accuracy: 1.0000
Epoch 14/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 1.4729e-05 - accuracy: 1.0000
Epoch 15/20
18000/18000 [==============================] - 81s 5ms/sample - loss: 8.5363e-06 - accuracy: 1.0000
Epoch 16/20
18000/18000 [==============================] - 81s 5ms/sample - loss: 5.2477e-06 - accuracy: 1.0000
Epoch 17/20
18000/18000 [==============================] - 80s 4ms/sample - loss: 3.2848e-06 - accuracy: 1.0000
Epoch 18/20
18000/18000 [==============================] - 81s 5ms/sample - loss: 2.1174e-06 - accuracy: 1.0000
Epoch 19/20
18000/18000 [==============================] - 81s 4ms/sample - loss: 1.6288e-06 - accuracy: 1.0000
Epoch 20/20
18000/18000 [==============================] - 82s 5ms/sample - loss: 9.4652e-07 - accuracy: 1.0000
Train set accuracy: 1.0
Test set accuracy: 1.0

While we have a nice and stable model with respect to the training set, let’s see if we can speed up the learning to attain a lower loss with less epochs. We would like to improve the algorithm’s convergence speed toward the global minimium. We can try to introduce Batch Normalisation to the 3rd axis (the channel axis).

# getting the train and test set
x_train_nn = fingers_dataset['np_train']['X'].copy()
x_train_nn = x_train_nn.reshape((x_train_nn.shape[0],x_train_nn.shape[1],x_train_nn.shape[2],1))
y_train_nn = to_categorical(y_train_digit)
x_test_nn = fingers_dataset['np_test']['X'].copy()
x_test_nn = x_test_nn.reshape((x_test_nn.shape[0],x_test_nn.shape[1],x_test_nn.shape[2],1))
y_test_nn = to_categorical(y_test_digit)

# input - we're giving the size of the image, i.e. we're making the input layer have 16,384 neurons
X_input = Input(shape=(x_train_nn.shape[1:]))

# convolutional layer
X = Conv2D(64,kernel_size=4,strides=2)(X_input)
X = BatchNormalization(axis=3)(X)
X = Activation('relu')(X)

# convolutional layer
X = Conv2D(32,kernel_size=3,strides=2)(X)
X = BatchNormalization(axis=3)(X)
X = Activation('relu')(X)

X = Flatten()(X)

# adding another fully connected layer
X = Dense(6, activation='softmax', name='fc')(X)

# the model
model_CNN_BatchNorm = Model(inputs = X_input, outputs = X, name='CNNModel_with_batch_norm')

# compile
model_CNN_BatchNorm.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ["accuracy"])
print(x_train_nn.shape,y_train_nn.shape)
# fit
model_CNN_BatchNorm.fit(x_train_nn,y_train_nn,batch_size=32,epochs=20)

preds = model_CNN_BatchNorm.evaluate(x_train_nn,y_train_nn,verbose=0)
print('Train set accuracy:',preds[1])

preds = model_CNN_BatchNorm.evaluate(x_test_nn,y_test_nn,verbose=0)
print('Test set accuracy:',preds[1])

predictions = model_CNN_BatchNorm.predict(x_test_nn)
predictions = tf.argmax(predictions, axis=1).numpy()
actuals = tf.argmax(y_test_nn, axis=1).numpy()

x_incorrectly_classified = x_test_nn[(predictions != actuals)]
y_incorrectly_classified = np.argmax(y_test_nn[(predictions != actuals)],axis=-1)
y_predicted = predictions[(predictions != actuals)]

for i in range(len(y_predicted)):
    # display the image using the numpy array
    plt.imshow(x_incorrectly_classified[i].reshape(fingers_dataset['np_train']['X'].shape[1:]))
    plt.show()
    print('Prediction:{}, actual:{}'.format(y_predicted[i],y_incorrectly_classified[i]))

(18000, 128, 128, 1) (18000, 6)
Train on 18000 samples
Epoch 1/20
18000/18000 [==============================] - 246s 14ms/sample - loss: 0.0695 - accuracy: 0.9863
Epoch 2/20
18000/18000 [==============================] - 244s 14ms/sample - loss: 9.2048e-05 - accuracy: 1.0000
Epoch 3/20
18000/18000 [==============================] - 237s 13ms/sample - loss: 3.8142e-05 - accuracy: 1.0000
Epoch 4/20
18000/18000 [==============================] - 239s 13ms/sample - loss: 2.1835e-05 - accuracy: 1.0000
Epoch 5/20
18000/18000 [==============================] - 257s 14ms/sample - loss: 1.4021e-05 - accuracy: 1.0000
Epoch 6/20
18000/18000 [==============================] - 267s 15ms/sample - loss: 9.3828e-06 - accuracy: 1.0000
Epoch 7/20
18000/18000 [==============================] - 255s 14ms/sample - loss: 6.7856e-06 - accuracy: 1.0000
Epoch 8/20
18000/18000 [==============================] - 247s 14ms/sample - loss: 5.0618e-06 - accuracy: 1.0000
Epoch 9/20
18000/18000 [==============================] - 243s 14ms/sample - loss: 3.6146e-06 - accuracy: 1.0000
Epoch 10/20
18000/18000 [==============================] - 242s 13ms/sample - loss: 2.7530e-06 - accuracy: 1.0000
Epoch 11/20
18000/18000 [==============================] - 247s 14ms/sample - loss: 2.0065e-06 - accuracy: 1.0000
Epoch 12/20
18000/18000 [==============================] - 242s 13ms/sample - loss: 1.5438e-06 - accuracy: 1.0000
Epoch 13/20
18000/18000 [==============================] - 240s 13ms/sample - loss: 1.1467e-06 - accuracy: 1.0000
Epoch 14/20
18000/18000 [==============================] - 241s 13ms/sample - loss: 8.7752e-07 - accuracy: 1.0000
Epoch 15/20
18000/18000 [==============================] - 240s 13ms/sample - loss: 6.6278e-07 - accuracy: 1.0000
Epoch 16/20
18000/18000 [==============================] - 244s 14ms/sample - loss: 5.0166e-07 - accuracy: 1.0000
Epoch 17/20
18000/18000 [==============================] - 240s 13ms/sample - loss: 3.8083e-07 - accuracy: 1.0000
Epoch 18/20
18000/18000 [==============================] - 243s 14ms/sample - loss: 2.8649e-07 - accuracy: 1.0000
Epoch 19/20
18000/18000 [==============================] - 237s 13ms/sample - loss: 2.1698e-07 - accuracy: 1.0000
Epoch 20/20
18000/18000 [==============================] - 237s 13ms/sample - loss: 1.6394e-07 - accuracy: 1.0000
Train set accuracy: 1.0
Test set accuracy: 1.0

Notice how we’ve achieved a lower loss after fewer epochs compared to the CNN without Batch Normalisation. But most importantly we have a model which is more stable in its learning. We now have exceptional performance as well as stability in the convergence. We can look at a summary of our final model:

model_CNN_BatchNorm.summary()

Model: "CNNModel_with_batch_norm"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_7 (InputLayer)         [(None, 128, 128, 1)]     0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 63, 63, 64)        1088      
_________________________________________________________________
batch_normalization_3 (Batch (None, 63, 63, 64)        256       
_________________________________________________________________
activation_5 (Activation)    (None, 63, 63, 64)        0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 31, 31, 32)        18464     
_________________________________________________________________
batch_normalization_4 (Batch (None, 31, 31, 32)        128       
_________________________________________________________________
activation_6 (Activation)    (None, 31, 31, 32)        0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 30752)             0         
_________________________________________________________________
fc (Dense)                   (None, 6)                 184518    
=================================================================
Total params: 204,454
Trainable params: 204,262
Non-trainable params: 192
_________________________________________________________________

The evolution of our model through the epochs shows us the speed of learning. Let’s compare our unstable Neural Networks (with/without batch norm) with our CNNs (with/without batch norm):

fig, axes = plt.subplots(nrows=4,sharex=True,figsize=(10,10))

axes[0].plot(model_CNN_BatchNorm.history.history['loss'],label=model_CNN_BatchNorm.name,c='b')
axes[1].plot(model_CNN.history.history['loss'],label=model_CNN.name,c='black')
axes[2].plot(model_NN_batchNorm.history.history['loss'],label=model_NN_batchNorm.name,c='y')
axes[3].plot(model_NN.history.history['loss'],label=model_NN.name,c='g')

axes[0].set_ylim(-0.01,0.1)
axes[1].set_ylim(-0.01,0.1)
axes[2].set_ylim(-0.01,0.1)
axes[3].set_ylim(-0.01,0.1)

axes[0].legend()
axes[1].legend()
axes[2].legend()
axes[3].legend()

axes[3].set_xlabel('Epochs')

axes[0].set_ylabel('Loss')
axes[1].set_ylabel('Loss')
axes[2].set_ylabel('Loss')
axes[3].set_ylabel('Loss')

The CNN with batch norm is the most stable model.

We now have a high performing stable model we would like to save (save the architecture and parameters) so that we can load it whenever we need to apply it.

# Save the model
model_CNN_BatchNorm.save(model_h5_save)

# load the model
fingers_model = load_model(model_h5_save)

fingers_model.summary()

Model: "CNNModel_with_batch_norm"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_7 (InputLayer)         [(None, 128, 128, 1)]     0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 63, 63, 64)        1088      
_________________________________________________________________
batch_normalization_3 (Batch (None, 63, 63, 64)        256       
_________________________________________________________________
activation_5 (Activation)    (None, 63, 63, 64)        0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 31, 31, 32)        18464     
_________________________________________________________________
batch_normalization_4 (Batch (None, 31, 31, 32)        128       
_________________________________________________________________
activation_6 (Activation)    (None, 31, 31, 32)        0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 30752)             0         
_________________________________________________________________
fc (Dense)                   (None, 6)                 184518    
=================================================================
Total params: 204,454
Trainable params: 204,262
Non-trainable params: 192

Next Time

Here we have developed a model to successfully classify the number of fingers on a hand in an image. We still have an outstanding task – to classify whether the hand is a left hand or a right hand. Since we have saved the model developed here, we can load it and use the learning of this model to apply to the new classification task (Transfer Learning). The reason we can do this is that the features learned in this model are highly likely to be useful for classifying the hand side. The only additional step we will have to do is to replace the output layer of this model with an output layer for a binary classification task.

TaggedClassification Convolutional Neural Networks Image Classification Neural Networks