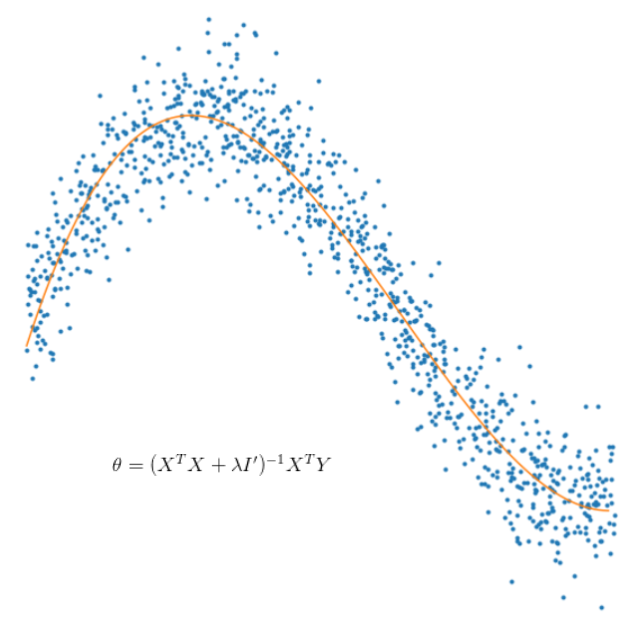
Ridge Regression

Before introducing Ridge Regression, let’s have a brief look at Linear Regression. Linear Regression is one of the simplest yet fundamental statistical learning techniques. It is a great initial step towards more advanced and computationally demanding methods.

Linear regression examines the relationship between a dependent variable and one or more independent variables. Linear regression with p independent variables focuses on fitting a straight line in p+1-dimensions that passes as close as possible to the data points in order to reduce error.

General Characteristics of Linear Regression:

A supervised learning technique
Useful for predicting a quantitative response
Attempts to fit a function to predict a response variable
The problem is reduced to a parametric problem of finding a set of parameters
The function shape is limited (as a function of the parameters)

The idea behind Linear Regression is that we reduce the problem of estimating the response variable, Y, by assuming there is a linear function of the predictor variables, X1, X2,… which describes Y. This reduces the problem to that of solving for the parameters β0, β1, β2, …, βn in the equation:

The βs are the parameters, and the Xs are the predictors. ϵ is a random error term and is assumed to be normally distributed

With a single predictor, we are expected to fit a function to the data similar to the following:

But allowing predictors of higher orders, it is possible to fit a non-linear function of the original predictors:

The original function generating the data points is a sine curve. The linear regression form includes the predictors X, X^2 and X^3

The above equation for the assumption of the shape of the function is called the hypothesis function and this can be written in matrix notation as (θ is used here instead of β)

The hypothesis function for Linear Regression in matrix notation. X is an n by (p+1) matrix and θ is a (p+1) by 1 vector. Including the constant term is what results in an extra column in X filled with all 1s

We are looking to find a vector θ which minimises the errors between the values given by the hypothesis function (the orange line in the graphs above) and the actual response variables on known data. Mathematically, the equation we need to minimise is

The Cost function for Linear Regression. The last step is the index representation of the previous step. Also, $(X\theta)^T Y = Y^T(X\theta)$ . $e_i$ is the error resulting from the $i_{th}$ prediction and the $i_{th}$ actual value, $h_{\theta}(X^{(i)}) - Y^{(i)}$ .

Now we can find the derivative of the Cost function thanks to the index representation since all terms are scalar

The derivative of the Cost function is a vector of derivatives

Setting this to zero and solving

Putting the solution back into matrix notation

The extra step we will be taking here to introduce Ridge Regression is to add an additional term in this equation which is the L2-norm

$\lambda || \theta ||^2 = \lambda \sum_{i=1}^n \theta_i^2 = \lambda \theta'^T \theta' = \lambda \theta_j' \theta_j'$

where $\theta'$ is the parameter vector $\theta$ but with the first term corresponding to the coefficient of the constant term set to zero and $\lambda$ is a scaling factor or shrinkage factor. The reason we do this is that we only want to constrain the coefficients of the predictors and not the constant term. Adding the L2-norm to the Cost function serves to constrain the parameters while minimising the error. The shrinkage factor controls how much emphasis we want to put on constraining the parameters. With this L2 norm, the Cost function then becomes

$J(\theta)=\theta_j x_{ji} x_{ij} \theta_j - 2\theta_j x_{ji} y_i + y_i^2 + \lambda \theta_j'^2$

Differentiating, and setting to zero, the solution then is slightly different from that for Linear Regression

$\theta = (X^T X + \lambda I')^{-1} X^T Y$

where $I'$ is the identity matrix with the top left corner 0. If we set λ = 0 in the above solution for θ we recover the Linear Regression solution. In Python code this looks as follows

L = 0.2
normalize = False

# Convert the predictor dataframe and the response dataframe to arrays to be consistent with data type
X = np.concatenate((np.ones((X.shape[0],1)),np.array(X)),axis=1)
y = np.array(y)

ncols = X.shape[1]

if normalize:
    # standardise X if required - Can be vectorised using broadcasting
    for i in range(1,ncols):
        X[:,i] = (X[:,i] - np.mean(X[:,i]))/np.std(X[:,i])

    # standardise y if required
    y = (y - np.mean(y))/np.std(y)

# Create transpose (3 X n)
X_T = X.transpose()

# Calculate X^T X (3 X 3)
XTX = X_T.dot(X)

# Create I'
Id = np.eye(XTX.shape[0])
Id[0,0] = 0

# Add the shrinkage factor part
XTX = XTX + L*Id

# calculate inverse of XTX + lambda I' (3 X 3)
XTX_inv = np.linalg.inv(XTX)

# Calculate theta
theta = XTX_inv.dot(X_T.dot(y))

Now that we have the calculation for θ, we can look at the p-values corresponding to the θ‘s

Let $\hat{\theta}$ be an unbiased estimator of $\theta$ and $\hat{Y}$ be the fitted values for $Y$ . i.e. we expect that $E[\hat{\theta}]=\theta$ and $E[ \hat{Y} ]=Y$ . Then the variance of the estimator can be calculated as follows

where $\hat{Y} - Y = e$ are the residuals

where $\hat{Y} - Y = e$ are the residuals

and

The Mean Squared Error with p predictors

In Python code (where ridgeModel is our fitted statsmodels.api Ridge Regression model)

# Get the coefficient solutions from the model
coefs = np.append(ridgeModel.params[0],ridgeModel.params[1:])

# Get the predictions (X_new includes the constant term)
predictions = ridgeModel.predict(X_new)

# Calculate the MSE
MSE = (sum((y-predictions)**2))/(len(X_new)-len(X_new.columns))

# Calculate the variance
var = MSE*(np.linalg.inv(np.dot(X_new.T,X_new)).diagonal())

# Calculate the standard deviation
sd = np.sqrt(var)

# Calculate the t-statistics
t = coefs/ sd

# Calculate the p-values using the t-statistics and the t-distribution (2 is two-sided)
p_values =[2*(1-stats.t.cdf(np.abs(i),(len(X_new)-1))) for i in t]

# 3 decimal places to match statsmodels output
var = np.round(var,3)
t = np.round(t,3)
p_values = np.round(p_values,3)

# 4 decimal places to match statsmodels
coefs = np.round(coefs,4)

summary_df = pd.DataFrame()
summary_df["Features"],summary_df["coef"],summary_df["std err"],summary_df["t"],summary_df["P > |t|"] = [
    X_new.columns,coefs,sd,t,p_values]
print(summary_df)

We can extend the Ridge class of SKLearn to give it the ability to calculate p-values (full class at the end of this article). This module can either be found here or simply install the package from PyPi as follows

pip install model_arena

Then import and use it as follows on a housing dataset as an example (found here )

# The module containing our custom RidgeRegression class
from model_arena import RidgeRegression

# Predictor variables
X = housePrice.drop('SalePrice',axis=1)

# Response variable
y = housePrice['SalePrice']

# Create a RidgeRegression object
rm = RidgeRegression()

# Run the feature selection method as above to limit to the most important variables. 
# Stores the order of variables to the object
rm.featureSelection(X,y)

# Find the value of alpha minimising MSE for these features
rm.findBestAlpha(X[rm.bestMeanCVModel],y)

# Print the alpha
print('Alpha = {}'.format(rm.alpha))

# Fit the model with the best features and the alpha
rm.fit(X[rm.bestMeanCVModel],y)

# Display a summary including p-values
rm.summary(X[rm.bestMeanCVModel],y)

This will produce an output similar to the following (note that ‘MSE’ and ‘Negative MSE’ are used interchangeably here. SKLearn uses ‘Negative MSE’)

The output is designed to look similar to statsmodels.api and setting the shrinkage factor alpha=0 should recover the statsmodels.api output for Linear Regression (note the shrinkage factor lambda is called alpha in SKLearn’s Ridge class)

This is the statsmodels.api p-value output on the housing dataset using Linear Regression

This is the Ridge Regression output for the same housing dataset when setting alpha (shrinkage factor) = 0

Running Ridge Regression with alpha = 0 and then with an optimised alpha as above, it can be seen that it is possible to improve on Linear Regression MSE as well as reduce the variance of the predictions from the model. In code

# Compare summary outputs between Ridge Regression and Linear Regression
print('RIDGE REGRESSION SUMMARY')
rm.summary(X_train,y_train)

print('\n\nLINEAR REGRESSION SUMMARY')
rmlm = RidgeRegression(alpha=0)
rmlm.fit(X_train,y_train)
print('Parameters of the linear regression model = {}'.format([rmlm.intercept_,rmlm.coef_]))
rmlm.summary(X_train,y_train)

# Predict a new set of points and find MSE for Linear Regression and Ridge Regression

print('Linear Regression MSE = {}'.format((rmlm.predict(X_test) - y_test).dot(rmlm.predict(X_test) - y_test)))
print('Ridge Regression MSE = {}'.format((rm.predict(X_test) - y_test).dot(rm.predict(X_test) - y_test)))

# Confirm that the standard deviation of predictions is smaller for Ridge Regression than for Linear Regression

rmpredictions = []
for i,j in list(zip(list(X_test.values),list(y_test))):
    rmpredictions.append(rm.predict(i.reshape(1,-1)))
    
rmlmpredictions = []
for i,j in list(zip(list(X_test.values),list(y_test))):
    rmlmpredictions.append(rmlm.predict(i.reshape(1,-1)))
    
print('Standard deviation of Linear Regression predictions = {}'.format(np.std(rmlmpredictions)))
print('Standard deviation of Ridge Regression predictions = {}'.format(np.std(rmpredictions)))

A more in-depth investigation can be found here and an application of Linear/Lasso/Ridge regression on Kaggle’s housing dataset can be found here.

Summary

We have seen the following:

Ridge Regression is an extension of Linear Regression by constraining the coefficients in the Cost function.
Ridge regression reduces the variance of the predictions it provides
Setting the shrinkage factor to zero in Ridge Regression means the Cost function is identical to that of Linear Regression and thus the results are identical too
It is possible to extend SKLearn’s Ridge class (example given at the end of this article) to also calculate p-values for Ridge Regression

Supplementary Material

class RidgeRegression(Ridge):
    '''
    This class inherits from the Ridge class in the sklearn package. It extends that class by
    adding the capability to produce p-values, run feature selection and find the best alpha
    which minimises the MSE
    '''
    
    def summary(self,X,y):
        '''
        This method produces a summary similar to the one produced by statsmodels.api.
        It includes the coefficients and their p-values in a summary table
        :param X: features array
        :param y: response array
        '''
        
        # This will store the coefficients of the model that has already been run
        coefs = []
        
        # If the model was fit with an intercept
        if 'intercept_' in dir(self):
            coefs = np.append(self.intercept_,self.coef_)
        else:
            coefs = self.coef_

        # Get the predictions
        predictions = self.predict(X)

        # If a constant column needs to be added (determine this dynamically)
        if len(X.columns) < len(coefs):
            X = X.copy()
            X.insert(0,'Const',1)
        
        # Calculate the MSE
        MSE = (sum((y-predictions)**2))/(len(X)-len(X.columns))

        # Calculate the variance
        var = MSE*(np.linalg.inv(np.dot(X.T,X)).diagonal())

        # Calculate the standard deviation
        sd = np.sqrt(var)

        # Calculate the t-statistics
        t = coefs/ sd

        # Calculate the p-values using the t-statistics and the t-distribution (2 is two-sided)
        p_values =[2*(1-stats.t.cdf(np.abs(i),(len(X)-1))) for i in t]

        # 3 decimal places to match statsmodels output
        var = np.round(var,3)
        t = np.round(t,3)
        p_values = np.round(p_values,3)

        # 4 decimal places to match statsmodels
        coefs = np.round(coefs,4)
        
        # Summary dataframe
        summary_df = pd.DataFrame()
        summary_df["Features"],summary_df["coef"],summary_df["std err"],summary_df["t"],summary_df["P > |t|"] = [X.columns,
                                                                                                    coefs,sd,t,p_values]
        print(summary_df) 
        
    def findBestAlpha(self,X,y,silent=True):
        '''
        This method keeps changing alpha until the MSE is reduced as much as it can be reduced. This
        alpha selection depends on input datasets
        :param X: features array
        :param y: response array
        :param silent: if True, then progress is omitted
        '''

        silent = True
        alpha = 1
        prevAlpha = None
        bestMSE = None
        tol = 0.000001
        doublingMode = True
        
        # Here, we start by continuously doubling alpha until we get to a point where the MSE doesn't increase
        # Then, at this point, we switch to incrementing (or decrementing) by smaller amounts until the tolerance is reached
        while True:
            # Calculate the MSE using this alpha
            thisMSE = np.mean(cross_val_score(RidgeRegression(alpha=alpha),X,y,scoring='neg_mean_squared_error',cv=10))

            if not silent:
                print('alpha = {}\nbestMSE = {}\nthisMSE = {}\n#############'.format(alpha,bestMSE,thisMSE))

            # if doubling mode
            if doublingMode:
                # update bestMSE
                if (not bestMSE) or (bestMSE < thisMSE):
                    bestMSE = thisMSE
                else:
                    if not silent:
                        print('Doubling Finished!!!!')
                        
                    # switch the mode and roll back alpha to the previous one
                    doublingMode = False
                    tempAlpha = prevAlpha
                    prevAlpha = alpha
                    alpha = tempAlpha
                    continue

                # update alpha
                prevAlpha = alpha
                alpha = (alpha + 0.001)*2
            else:        
                # update alpha to |alpha-prevAlpha|/2 away from where it currently is (in either direction)
                ghostPoint = alpha + (alpha - prevAlpha)
                nextAlpha1 = (prevAlpha + alpha)/2
                nextAlpha2 = (alpha + ghostPoint)/2
                
                # The Ridge class has numerical issues when alpha is close to zero
                if(nextAlpha1 < 0.0001):
                    nextAlpha1 = 0.0001
                if(nextAlpha2 < 0.0001):
                    nextAlpha2 = 0.0001
                    
                # Calculate the MSE on either side of alpha
                MSE1 = np.mean(cross_val_score(RidgeRegression(alpha=nextAlpha1),X,y,scoring='neg_mean_squared_error',cv=10))
                MSE2 = np.mean(cross_val_score(RidgeRegression(alpha=nextAlpha2),X,y,scoring='neg_mean_squared_error',cv=10))

                # Choose to MSE and the corresponding alpha of the one that is better
                if (MSE1 > MSE2) and (MSE1 > bestMSE) and (np.abs(prevAlpha - alpha) > tol):
                    prevAlpha = alpha
                    alpha = nextAlpha1
                    bestMSE = MSE1
                elif (MSE2 > MSE1) and (MSE2 > bestMSE) and (np.abs(prevAlpha - alpha) > tol):
                    prevAlpha = alpha
                    alpha = nextAlpha2
                    bestMSE = MSE2
                else:
                    if (np.abs(prevAlpha - alpha) > tol):
                        # pull prevAlpha closer to alpha
                        prevAlpha = (prevAlpha + alpha)/2
                    else:
                        alpha = prevAlpha
                        break

        self.alpha = alpha
        print('Ridge Regression MSE = {}, best alpha = {}'.format(bestMSE,alpha))

    def featureSelection(self,X,y):
        '''
        This method iterates and adds a new feature to the features list in the
        order of best improvement of MSE
        :param X: features array
        :param y: response array
        '''
        
        # Run through each model in the correct order and run CV on it and save the best CV score
        bestMeanCV = -1
        bestMeanCVModel = []
        oldArraySize = 0

        columnsArray = X.columns.copy()

        while oldArraySize != len(X):
            bestPredictor = ''
            oldArraySize = len(X.columns)
            for i in columnsArray:
                thisModel = bestMeanCVModel.copy()
                thisModel.append(i)
                # First set X to be the full set of remaining parameters
                x = X.loc[:,thisModel]

                if len(x.columns) == 1:
                    linregCVScores = cross_val_score(Ridge(alpha=6),x.values.reshape(-1,1),y,scoring='neg_mean_squared_error',cv=10)
                else:
                    linregCVScores = cross_val_score(Ridge(alpha=6),x,y,scoring='neg_mean_squared_error',cv=10)

                if bestMeanCV > -linregCVScores.mean():
                    bestMeanCV = -linregCVScores.mean()
                    bestPredictor = i
                elif bestMeanCV == -1:
                    bestMeanCV = -linregCVScores.mean()
                    bestPredictor = i

            if bestPredictor not in columnsArray:
                break

            columnsArray = columnsArray.drop(bestPredictor)
            bestMeanCVModel.append(bestPredictor)
            print('{} was added with test MSE {}'.format(bestMeanCVModel[-1],bestMeanCV))


        self.bestMeanCVModel = bestMeanCVModel
        self.bestMeanCV = bestMeanCV
        print('The final best model is {} and its TEST MSE is {}'.format(bestMeanCVModel,bestMeanCV))

TaggedLinear Regression Python Regression Ridge Regression

Ridge Regression

Summary

Supplementary Material

Analysing online review data - Part 2

Gambler's Ruin