Time Series Analysis 1 – Identifying Structure

April 23, 2022 Regression Statistics Time Series

Time-series analysis is a statistical method of analyzing data from repeated observations on a single unit or individual at regular intervals over a large number of observations

Time Series Analysis – Velicer, W. F., & Fava, J. L. (2003)

Introduction

In this article we tackle a generated set of progressively more complex time series datasets. From a random series to an ARIMA series with seasonality as well as a series with a structural change. For each of these time series we apply the traditional techniques used in time series analysis to ascertain the underlying structure. In a follow up article we will make the final step to use what we’ve learned to forecast into the future.

Example Distributions

A series of generated time series data generated using the statsmodels.tsa package in Python. The name of each series is in the title. s and t are the seasonal period (in days) and trend gradient respectively. A trend of 0.01 means that the average is increasing by 0.01 per day.

Time Series Models

For a model ARMA(p,q), the AR coefficients have the form [1, -\phi_1, -\phi_2, ..., -\phi_p] and the MA coefficients have the form [1, \theta_1, \theta_2, ..., \theta_q].
An AR(p) model specifies that the time series can be modelled by:

x_t=\phi_{0} + \phi_{1} x_{t-1} + \phi_{2} x_{t-2}+... + \phi_{p} x_{t-p} + \epsilon_{t}

where \phi_0 is the mean and the \{\phi_i : i \geq 1\} are the coefficients and \epsilon_t \sim N(0,\sigma^2) is an error term. This implies that the relationship between x_{t-i} and x_{t} while keeping the effects of x_{t-j:j \neq i \& j<=p} constant can be expressed by the correlation coefficient \phi_{t-i}. This can also be written as:

(1- \phi_{1}B - \phi_{2}B^2 - ... - \phi_{p}B^p)x_t=\phi_{0} + \epsilon_{t}

where B^i is the backshift operator of order i (i.e. B^i x_t = x_{t-i}).

An MA(q) model specifies that the time series can be modelled by:

x_t=\theta_{0} + \epsilon_{t} + \theta_{1} \epsilon_{t-1} + \theta_{2} \epsilon_{t-2}+... + \theta_{q} \epsilon_{t-q}

where \theta_{0} is the mean, \epsilon_i \sim^{iid} N(0,\sigma^2) are error terms and \{\theta_i : i \geq 1\} are the coefficients. The can also be written as:

x_t=\theta_{0} + (1 + \theta_{1} B + \theta_{2} B^2 + ... + \theta_{q} B^q)\epsilon_{t}

Putting this together and adding a seasonal term with period s, a SARIMA(p,d,q,P,D,Q,s) model can be represented altogether as:

(1- \phi_{1}B - \phi_{2}B^2 - ... - \phi_{p}B^p)(1 - \phi_{s1}B^{s} - ... - \phi_{sP}B^{sP})(1 - B)^d (1 - B^s)^D x_t = m + (1 + \theta_{1} B + \theta_{2} B^2 + ... + \theta_{q} B^q)(1 + \theta_{s1}B^{s} + ... + \theta_{sQ}B^{sQ})\epsilon_{t}

In this model, the time series differenced d times and seasonally differenced D times is said to have AR order p with coefficients \phi_{i}, MA order q with coefficients \theta_{i}, Seasonal AR (SAR) order P with coefficients \phi_{si}, Seasonal MA (SMA) order Q with coefficients \theta_{si} and mean m.

Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF)

The autocorrelation function (ACF) is a statistical technique that we can use to identify how correlated the values in a time series are with each other. Autocorrelation is the correlation between a time series (signal) and a delayed version of itself, while the ACF plots the correlation coefficient against the lag, and it’s a visual representation of autocorrelation.

The partial autocorrelation function (PACF) is a statistical measure that captures the correlation between two variables after controlling for the effects of other variables. A partial autocorrelation function captures a β€œdirect” correlation between time series and a lagged version of itself.

https://www.baeldung.com/cs/acf-pacf-plots-arma-modeling

Both the ACF and the PACF will help us identify the p and q in ARMA(p,q). For example, if PACF shows an exponential decay in the coefficients of successive lags but ACF shows significant lags up until q inclusive, the time series has MA(q) characteristics. Examples of using the below table to understand the ARMA model is shown further down.

Adapted from https://www.youtube.com/watch?v=ZE_WGBe0_VU&t=134s.

Stationarity

The above table is only applicable to stationary time series. This is because two series that are not stationary can be found to have a spurious correlation even if they were randomly generated.
The time series x_t is stationary if:

  • x_t has a constant mean
  • x_t has a constant variance
  • x_t has no seasonality

If x_{t} has a non-constant mean, we can convert it into stationary x'_{t} by differencing

x'_{t}=x_{t}-x_{t-1}=(1-B)x_t

If it is still non-stationary, we can convert it again into stationary x''_{t} by differencing

x''_{t}=x'_{t}-x'_{t-1}=(1-B)^2 x_t

If x_{t} has seasonality, say with period s, we can remove the seasonality by computing

x'_{t}=x_{t}-x_{t-s}=(1-B^s)x_t

We can check for non-stationarity with the Augmented Dickey-Fuller Test (ADF) with the null hypothesis that the signal is non-stationary.

Model Selection with Akaike Information Criterion (AIC)

The Akaike information criterion (AIC) is an estimator of prediction error and thereby relative quality of statistical models for a given set of data. Given a collection of models for the data, AIC estimates the quality of each model, relative to each of the other models. Thus, AIC provides a means for model selection.

Wikipedia

Since the AIC is a measure of information loss, the model with the lowest AIC is the most likely candidate to represent the underlying data. Comparing the sum of squared errors between models via an F Test can also be used for model selection. However, AIC is more popular and easier because popular regression packages readily provide the AIC. Sometimes, a comparison of the MSE (mean squared error) on a hold out set provides a better approach to choosing the better model. Given a fitted time series model that properly represents the underlying structure, we expect the residuals to be random (devoid of patterns). To this end, the Ljung-Box test can help in testing for autocorrelation in the residuals.

Here is a summarised list of metrics we will use:

  • AIC: The level of confidence we have on out-of-sample performance
  • Test MSE: An estimate of out-of-sample performance
  • Ljung-Box: The level of confidence of whether the model really does represent the underlying structure (i.e. residuals are not correlated)

Given these definitions, we prefer to find time series models with unrelated residuals that have low AIC and Test MSE. Often, the model with the best AIC will not be the model with the best Test MSE. This is because the test set may not look like the historical data. A rule of thumb we’ll apply is that we choose models by considering both AIC and Test MSE. If the model with the smallest AIC produces a Test MSE that is significantly greater than the Test MSE of the second best AIC, it might make more sense to choose the model with the second best AIC.

Approach

The approach taken here to identify the underlying structure in the time series will be as follows:

  1. Test or observe if the fluctuations are getting bigger – variation in the variance (i.e. like in stock prices) – or if there is seasonality
    • If the fluctuations are getting bigger then transform the dataset (i.e. use log transform/log return)
    • If there is seasonality then difference
  2. Test or observe if there is any trend (AD Fuller)
    • If there is trend then use differencing
  3. Test if there are any autocorrelation terms
    • Use the Ljung-Box test
  4. Plot the ACF
    • To inform on the MA order
    • To inform on the SMA order
  5. Plot the PACF
    • To inform on the AR order
    • To inform on the SAR order
  6. Keep in mind a parsimony principle
    • e.g. p+d+q+P+D+Q <= 8
  7. Apply all candidate models to the data and report the following
    • AIC (over entire dataset)
    • Test MSE (over test set)
    • Ljung-Box on the residuals (over entire dataset)
  8. Select the best model keeping the following in mind
    • You should select the model with the lowest AIC which is simple. Balance complexity with AIC reduction
    • You should select the model with the lowest MSE which is simple. Balance complexity with MSE reduction
    • The model you select should have non-significant Ljung-Box p-value on the residuals to indicate lack of autocorrelation in residuals
  9. Fit your final model and forecast

Some Example Time Series

At the beginning of this note, several time series were generated by first specifying the model. Here, we use the generated data from each of those models to identify the model that generated them.

Random

Here’s the Random time series. This is a SARIMA(0,0,0,0,0,0,0) time series because according to the notation described at the beginning of the article, p=d=q=P=D=Q=0 and you have x_t=\epsilon_t:

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a non-significant p-value indicating not enough evidence for autocorrelation. But we will continue as if we’re trying to construct a time series model anyway

4/5- The ACF and PACF for the lags are shown below:

The coefficients for lag 0 is always 1. The shaded region represents the 95% confidence interval for the coefficients. There are no coefficients corresponding to lags 1+ that are significant. Indicating there are no AR/MA components

From the plots we can see there are no significant ACF or PACF coefficients (lag 1+). Checking the Golden Table For ARMA Identification, this time series has no AR component nor does it have an MA component. The output from an ARIMA regression model can be seen below. It shows a random component with significant variance \sigma^2 \simeq 1 but zero mean (const). Incidentally, all the time series were generated with 0 mean and 1 variance.

6- This model adheres to our parsimony principle (order 8 or less)

7- There is only a single candidate model so there aren’t any to choose between

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(0,0,0,0,0,0,0) and is expressed as:

x_t=\epsilon_t

where \epsilon_t \sim N(0,1.03).

AR(1) Model

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

We can see that in the ARMA identification table, this is most likely an AR(1). We can also see from the below regression that the coefficient of AR lag 1 is roughly 0.9 and is significant. This gives us further evidence that an AR(1) component exists.

6- This model adheres to our parsimony principle (order 8 or less)

7- There is only a single candidate model so there aren’t any to choose between

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(1,0,0,0,0,0,0) and is expressed as:

(1-\phi_1 B)x_t=\epsilon_t
where:
\phi_1=0.9
\epsilon_t \sim N(0,1.03)

AR(2) Model

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

The ACF is decaying while for the PACF we have a_k=0 \forall k > 2.

We see exponential decay for ACF (oscillating decay) and PACF coefficients drop to 0 after p=2. Checking the table this corresponds to a AR(2) time series. This series was infact generated using an AR = [1,-0.9,0.9] component. These coefficients can be seen in a regression below:

6- This model adheres to our parsimony principle (order 8 or less)

7- There is only a single candidate model so there aren’t any to choose between

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(2,0,0,0,0,0,0) and is expressed as:

(1-\phi_1 B-\phi_2 B^2)x_t=\epsilon_t
where:
\phi_1=0.92
\phi_2=-0.9
\epsilon_t \sim N(0,1.03)

MA(1) Model

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

The PACF is decaying while for the ACF we have m_k=0 \forall k > 1.

The PACF shows exponential decay while the ACF shows lags q > 1 are zero. According to the table this is an MA(1) time series. This series was in fact generated using an MA = $[1,0.9]$ component. This can also be seen in the below regression:

6- This model adheres to our parsimony principle (order 8 or less)

7- There is only a single candidate model so there aren’t any to choose between

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(0,0,1,0,0,0,0) and is expressed as:

x_t=(1+\theta_1 B) \epsilon_t
where:
\theta_1=0.93
\epsilon_t \sim N(0,1.03)

MA(4) Model

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

The PACF is “probably” decaying while for the ACF we have m_k=0 \forall k > 4.

The ACF shows lag coefficients are zero after q = 4. The PACF can be seen to show decay. According to the table this is an MA(4) series. However, this could also be an ARMA(2,4) time series if there is no agreement about the decay of PACF. We can look at the regression results for all candidate models

6- These models all adhere to our parsimony principle (order 8 or less) because the maximum order there could be is 2+4=6

7- We choose between all candidate models considering their AIC, Test MSE and Ljung-Box test results:

We choose model 9 in the image above because out of all models with a Ljung-Box test indicating no patterns in the residuals it has the lowest AIC and lowest Test MSE.

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(0,0,4,0,0,0,0) and is expressed as:

x_t=(1+\theta_1 B+\theta_2 B^2+\theta_3 B^3+\theta_4 B^4) \epsilon_t
where:
\theta_1=0.56
\theta_2=0.59
\theta_3=0.62
\theta_4=0.85
\epsilon_t \sim N(0,1.12)

ARMA(1,1) Model

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

The ACF could be decaying or m_k=0 \forall k > 2 while for the PACF we have a_k=0 \forall k > 1.

From the plots we have zero lags for q > 2 (ACF) and p > 1 (PACF). So this is an ARMA(1,2) series. Note that this could also be an ARMA(1,1) series if we choose not to consider the ACF lag 2 as well as an AR(1) series if we consider the ACF as a decay and also it could be an ARMA(2,2) series if we consider the PACF as having 2 significant lags. We will need to check the metrics for each of these models.

6- These models all adhere to our parsimony principle (order 8 or less) because the maximum order there could be is 2+2=4

7- We choose between all candidate models considering their AIC, Test MSE and Ljung-Box test results:

Here, the top most parsimonious models (degree/order < 3) are all comparable. We have chosen model 4 (AR(1,1)) because model 5 shows an increase in the Test MSE and AIC. But in reality any of these are suitable models. Another way to justify a selection of AR(1,1) can be seen below:

We can see from these regressions that ARMA(1,2) is out of the question. To decide on whether AR(1) or AR(1,1) is most likely the case, we consider if there is sufficient evidence that the more complex model (AR(1,1)) has a significant increase in Sum of Squared Residuals from the simpler model (AR(1)).

By performing an F-Test on the SSE from the simplest model, AR(1) and the more complex model, ARMA(1,1), we find evidence at the 0.05 significance level that the data supports ARMA(1,1). However, there is not enough evidence to support the most complex ARMA(1,2) model. This series was generated using AR = $[1,-0.3]$ and MA = $[1,0.2]$ components (Note: The 0th element always represents lag 0 which always has a coefficient of 1; The AR components are negative in the AR equation used here as shown at the beginning of the article).

8- Our time series model is 𝑆𝐴𝑅𝐼𝑀𝐴(1,0,1,0,0,0,0)Β and is expressed as:

(1-\phi B)x_t=(1+\theta_1 B) \epsilon_t
where:
\phi_1=0.36
\theta_1=0.19
\epsilon_t \sim N(0,1.03)

ARMA(2,6) Model

1- There looks to be constant variance

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

The ACF could be m_k=0 \forall k > 6 while for the PACF we have a_k=0 \forall k > 2 or a_k=0 \forall k > 1.

From the plots we have zero lags for q > 6 (ACF) and p > 2 (PACF). So this could be a ARMA(2,6) series. Note that the ACF does not show a decay. There is the question as to whether PACF lag 2 and ACF lag 6 are actually providing any tangible presence in the model. We look at comparing all candidate models

6- These models all adhere to our parsimony principle (order 8 or less) because the maximum order there could be is 2+6=8

7- We choose between all candidate models considering their AIC, Test MSE and Ljung-Box test results:

In the image above, we have decided to choose model 18 because while the assessment metrics are similar to model 20, model 18 is a simpler model of order 7.

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(1,0,6,0,0,0,0) and is expressed as:

(1-\phi B)x_t=(1+\theta_1 B+\theta_2 B^2+\theta_3 B^3+\theta_4 B^4+\theta_5 B^5+\theta_6 B^6) \epsilon_t
where:
\phi_1=0.52
\theta_1=0.02
\theta_2=0.24
\theta_3=0.21
\theta_4=0.28
\theta_5=0.37
\theta_6=0.46
\epsilon_t \sim N(0,1.15)

Note that a SARIMA(2,0,6,0,0,0,0) would also have modelled this time series well as evidence by the metrics of model 20 in the model selection image above. This is not surprising given that this series was generated as an ARMA(2,6).

ARMA(1,1) Model with seasonal period of 20 days

There is clear periodicity in the time series which needs to be removed

1- There looks to be constant variance but there is seasonality with period 20 as can be seen from the ACF plot. We remove the seasonality by differencing with shift 20

2- The time series doesn’t seem to have trend. Additionally, the time series is stationary according to an AD Fuller test at the 0.05 significance level

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

Here, we have a range of models to test. In addition to looking at models with p up to 2 and q up to 3, we also have the seasonal component to cater for as well as the differencing (we differenced to get rid of the seasonality). We know the seasonality period is 20. The peak at lag 20 in the ACF hints at a possible Q=1. Similarly, P can be up to 4 (peaks are observed up to lag 80 in the PACF). This gives a max order of 12 including both d=1 and D=1.

6- These models do not all adhere to our parsimony principle (order 8 or less) because the maximum order there could be is 12. We have to omit models with order greater than 8 to limit the complexity.

7- We choose between all candidate models considering their AIC, Test MSE and Ljung-Box test results:

Showing top 10 LB non-significant models ordered by AIC

In the image above, the best performing models in terms of AIC are of degree 6. This means we will not consider the worse performing models that are more complex. Here, we’ve chosen model 248, but model 274 is also a valid choice.

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(2,1,1,0,1,1,20) and is expressed as:

(1-\phi_1 B)(1-B)(1-B^{20})x_t=(1+\theta_1 B+\theta_2 B^2)(1+\theta_{s1} B^{20}) \epsilon_t
where:
\phi_1=0.56
\theta_1=-0.81
\theta_2=-0.18
\theta_{s1}=-0.997
\epsilon_t \sim N(0,1.05)

Note that a SARIMA(2,0,6,0,0,0,0) would also have modelled this time series well as evidence by the metrics of model 20 in the model selection image above. This is not surprising given that this series was generated as an ARMA(2,6).

AR(1) Model with trend

1- There looks to be constant variance with no seasonality

2- The time series clearly has trend. Additionally, the time series is not stationary according to an AD Fuller test at the 0.05 significance level (pvalue=0.06)

3- The Ljung-Box test shows a significant p-value (\sim 0) indicating enough evidence for autocorrelation. Here we will assume there exists a pattern to model

4/5- The ACF and PACF for the lags are shown below:

Looking at the ACF plot, the MA order (q) may range from 0 to 3. Looking at the PACF plot, the AR order (q) may range from 0 to 6. Adding the differencing (d=0,1) we have a max order of 10.

6- These models do not all adhere to our parsimony principle (order 8 or less) because the maximum order there could be is 10. We have to omit models with order greater than 8 to limit the complexity.

7- We choose between all candidate models considering their AIC, Test MSE and Ljung-Box test results:

Based on the image above, it’s an easy decision between the models as the model with the best AIC and Test MSE which also has a non significant Ljung-Box test is also the simplest model.

8- Our time series model is π‘†π΄π‘…𝐼𝑀𝐴(1,1,1,0,0,0,0) and is expressed as:

(1-\phi_1 B)(1-B)x_t=(1+\theta_1 B) \epsilon_t
where:
\phi_1=0.53
\theta_1=-0.96
\epsilon_t \sim N(0,1.07)

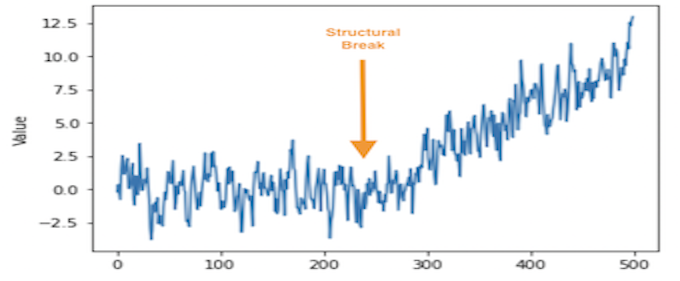
ARMA(1,1) Model with a structural break at t=250

This time series is not stationary according to an AD Fuller test. The decomposition shows a clear trend component in the second half of the series:

There is a structural break at time step around 250 due to a change in trend

Here we are going to investigate whether there is sufficient evidence for a structural/regime change at time step 250 via a Chow Test. First, we will try to identify the structure of the time series as a whole using the 8 step approach we’ve been applying.

The application of the 8 step approach on the entire time series of size 500 (Model 0), on the first 250 data points (Model 1) and the last 250 data points (Model 2) shows likely models of SARIMA(2,1,1,0,0,0,0), SARIMA(2,0,0,0,0,0,0) and SARIMA(2,1,1,0,0,0,0) respectively:

Though the coefficients are clearly different via observation, a Chow Test can be used to check for evidence of differences in these coefficients:

The Chow test has confirmed that there is sufficient evidence to support the hypothesis that time series 1 (data points up to 250) has a different structure that time series 2 (data points after 250).

Next Steps

After identifying the underlying structure of a time series to obtain a model most likely to represent it, the model can be used to forecast into the future (Time Series Analysis Part 2 – Forecasting).

Tagged

Naive Bayes

Time Series Analysis Part 2 - Forecasting