Time Series Analysis Part 2 – Forecasting

This article will walk through the steps in Time Series Analysis 1 – Identifying Structure and use this knowledge to forecast.

Visualising the Dataset (variance and seasonality)

This is the time series data:

Separating into train-test:

Here, out of a total of 500 data points, the first 400 will be used to fit a model to be tested on the final 100 to obtain the Test MSE (Mean Squared Error).

While it is clear there is constant variance, the seasonality is not so clear. A visualisation of the ACF (Autocorrelation Function) and PACF (Partial Autocorrelation Function) coefficients can be used to highlight any seasonality:

From the correlogram of the ACF coefficients, it can be seen that there exists seasonality with period 20. After removing this seasonality by differencing using lag 20 (shifting the rows by 20 then subtracting), the time series looks as follows:

Identifying Trend

It can be seen by eye in the plot of the time series data that there is no trend. But additional confirmation comes from an AD Fuller test for trend giving a p-value very close to zero. The null hypothesis in the AD Fuller test is that there is a unit root (trend). The alternative hypothesis is that there is no unit root. With a value close to zero, we move forward assuming there is no trend in the time series after removing seasonality via differencing.

Note that there may be both seasonality and trend but by removing the seasonality via differencing, the trend may also have been removed.

Identifying evidence of autocorrelation

After removing seasonality and trend it remains to understand whether there is a reason to investigate further the underlying structure of the time series data. This can be investigated via a Ljung-Box test and the corresponding p-value indicating the evidence against the null hypothesis that there is no autocorrelation.

The Ljung-Box test for this time series once the seasonality is removed results in a p-value very close to zero indicating evidence for autocorrelation. This supports the decision to move forward and identify further the underlying structure.

The underlying structure

To investigate the underlying structure of the time series, the ACF and PACF plots go a long way. While the ACF was previously used to help in the identification seasonality, they also inform as to the potential candidates for the order of the series. The plots of the ACF and PACF coefficients for the times series after the seasonality was removed is seen below:

There’s a lot of information in the ACF and PACF plots. From the ACF plot, it looks like the first 4 lag coefficients are significant. Beyond lag 4 there is no evidence for any significant coefficients. Previously, it was observed that the period for the seasonality is 20. Armed with this knowledge, from the ACF we can see that there is a peak at lag 20 with little evidence of significant peaks at later multiples of 20.

The PACF plot has many significant lags. This can sometimes occur and is an indication of the potential complexities time series data can contain. Lag 7 is highlighted here as being a reasonable order to consider. This does not mean that the best fitting model cannot have a PACF lag greater than 7 but what this informs is that the AR order has the potential to be large. Given the evidence of an MA order as well due to the ACF plot and existence of seasonality, it is unlikely that the resulting model will just involve an AR order. This implies that while the AR order is expected to be large, it has to be of a reasonable size because in combination with the other terms the model will otherwise risk being too complex.

The PACF plot also shows that there are 2 multiples of 20 (the seasonality period) that are significant.

Choosing the best model

The ACF and PACF plots from the previous section can be used to inform as to the potential candidates for model comparison. In the article Time Series Analysis 1 – Identifying Structure the importance of utilising multiple criteria in choosing a best model was demonstrated. Namely using the AIC on the entire time series, the MSE on the test set and the Ljung-Box test p-value on the residuals after the model is fit to the entire series. To clarify, both the AIC and the Ljung-Box test are performed on a model fit using the entirety of the dataset while the Test MSE is obtained from the test set by using a model fit to the training portion of the dataset. The thought here is that the AIC helps in estimating model fit on future data which is precisely what Test MSE is intended to do.

The candidates from the ACF and PACF plots are: p = [0,1,2,3,4,5,6,7], d = [0,1], q = [0,1,2,3,4], P = [0,1,2], D = [0,1], Q = [0,1], s = [20]. The meaning behind these variables can be found in Time Series Analysis 1 – Identifying Structure. It is clear that this is a complex time series but applying the parsimony principle and only models with order 12 or less will be considered (p+d+q+P+D+Q < 13). Additionally, only models that have a non-significant Ljung-box p-value (>0.05) on the residuals will be considered indicating that there is little evidence of patterns in the residuals. The top 25 models with a non-significant Ljung-Box p-value ordered by increasing AIC is shown below:

Analysing the table of results, it can be seen that the best performing model of order 12 is idx 852. This is true both when considering AIC as well as Test MSE. The next simpler model (order 11) results in an increase of both AIC and Test MSE that can be considered too great to justify a simplification of only 1 order. The much simpler model with idx 562 results in a Test MSE that is double that of idx 852 and so that model is not considered. However, model 614 may be a reasonable compromise given that in consolation for simplifying the order by 3, the Test MSE does not worsen (it actually improves) and the AIC is increased by a potentially reasonable amount.

Model 852 looks as follows:

If, by the parsimony principle, models with max order 9 were being considered our second model choice, model 614 looks as follows:

considering some of the other models which didn’t make the cut due to their large Test MSE, model 443 looks as follows:

And now model 324:

This highlights the importance of using multiple criteria to arrive at a reasonable identification of underlying structure. For example, model 324 reports a good AIC and additionally has little evidence suggesting patterns in the residuals. However, the Test MSE is more than double some of the other good performers. It is also clear here that the extend to which the Test MSE can help us in differentiating between models depends on the amount of data used for the test set. In the above plots of both model 324 as well as 443, the predictions begin to diverge further and further from the actual test set indicating that the Test MSE difference between good performing models and bad performing models gets greater the more test data we have.

Forecasting

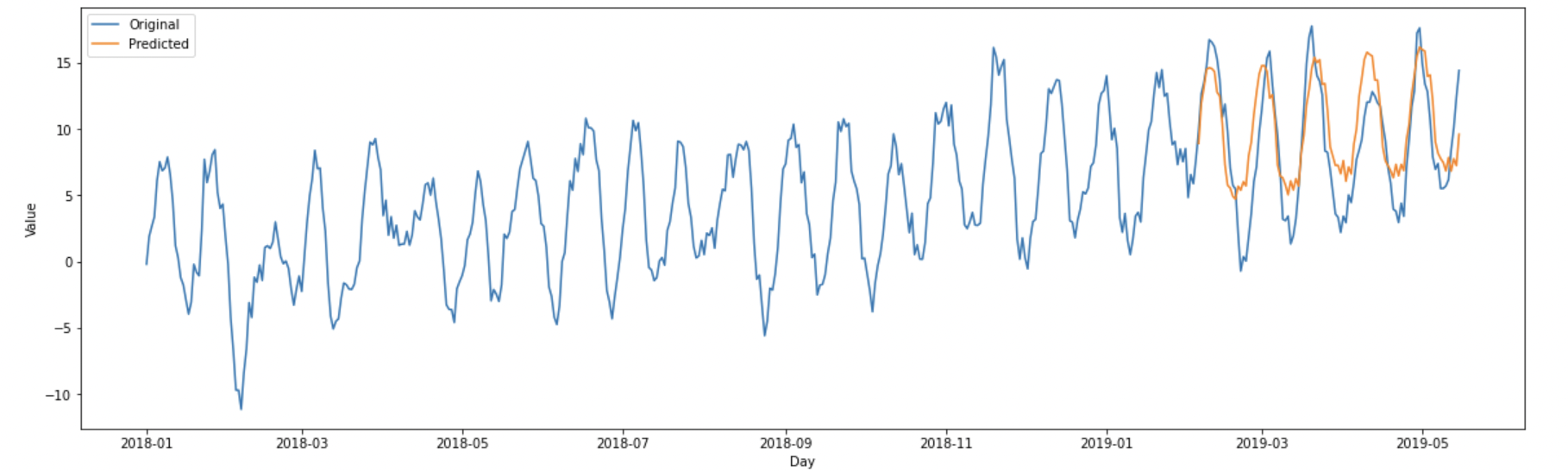
After identifying the model believed to be the best performing, it can be used to forecast into the future. The chosen model from the previous section is model 852 (SARIMA(5,1,4,0,1,1,20)). Using this model to forecast the next 100 datapoints (days) is shown below:

The time series model has clearly captured both the trend and the seasonality in the dataset.